SIMILAR RIGHT TRIANGLES

Two triangles are similar if two of their corresponding angles are congruent.

Example :

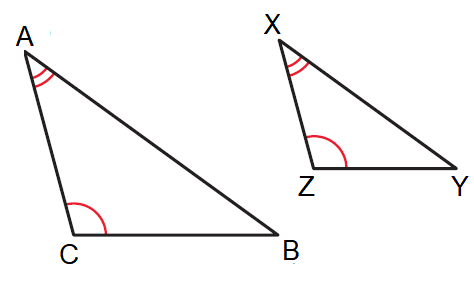
In the diagram shown above,

ΔABC ∼ ΔXYZ

Recall that the corresponding side lengths of similar triangles are in proportion.

Theorem

If the altitude is drawn to the hypotenuse of a right triangle, then the two triangles formed are similar to the original triangle and to each other.

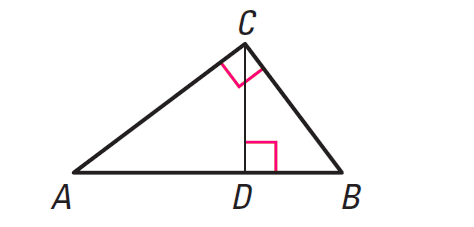
In the diagram shown above,

ΔCBD ∼ ΔABC

ΔACD ∼ ΔABC

ΔCBD ∼ ΔACD

Proof of the above Theorem :

Given : ΔABC is a right triangle ; altitude CD is drawn to hypotenuse AB.

To Prove :

ΔCBD ∼ ΔABC, ΔACD ∼ ΔABC, ΔCBD ∼ ΔACD

Proof :

First proof that ΔCBD ∼ ΔABC. Each triangle has a right angle, and each includes ∠B. The triangles are similar by the AA Similarity Postulate.

We can use similar reasoning to show that  ΔACD ∼ ΔABC.

To show that ΔCBD ∼ ΔACD, begin by showing that  ∠ACD ≅ ∠B because they are both complementary to ∠DCB. Then you can use the AA Similarity Postulate.

Using a Geometric Mean To Solve Problems

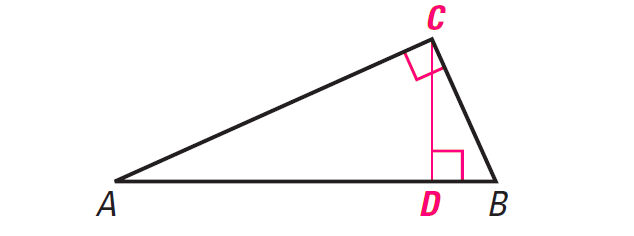
In right ΔABC shown above, altitude CD is drawn to the hypotenuse, forming two smaller right triangles they are similar to ΔABC. From the theorem given above, we know that ΔCBD ∼ ΔACD ∼ ΔABC.

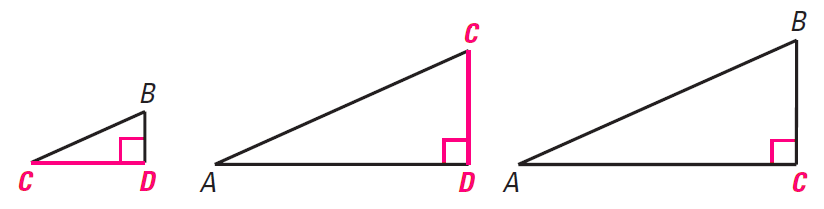
Notice that CD is longer leg of ΔCBD and the shorter leg ΔACD. When we write a proportion comparing the leg lengths of ΔCBD and ΔACD, we can see that CD is the geometric mean of BD and AD.

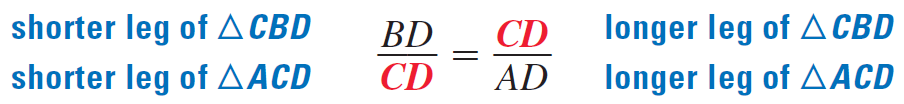
Sides CB and AC also appear in more than one triangle. Their side lengths are also geometric means, as shown by the proportions below :

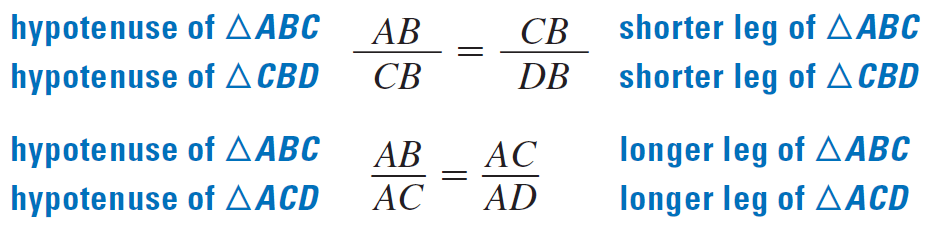
These results are expressed in the theorems below.

Geometric Mean Theorems

Theorem 1 :

In a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two segments.

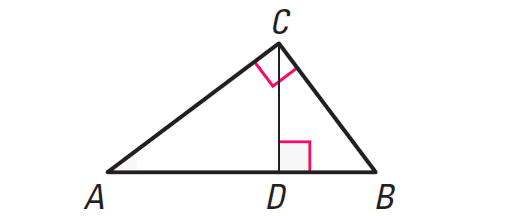
In the right ΔABC shown above, the length of the altitude CD is the geometric mean of the lengths of the two segments. AD and BD.

That is,

BD/CD = CD/AD

CD² = AD ⋅ BD

CD = √(AD ⋅ BD)

Theorem 2 :

In a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two segments.

The length of each leg of the right triangle is the geometric mean of the lengths of the hypotenuse and the segment of the hypotenuse that is adjacent to the leg.

In the right ΔABC shown above,

CB = √(AB ⋅ DB)

AC = √(AB ⋅ AD)

Finding the Height of a Roof

Example :

A roof has a cross section that is a right triangle. The diagram shows the approximate dimensions of this cross section.

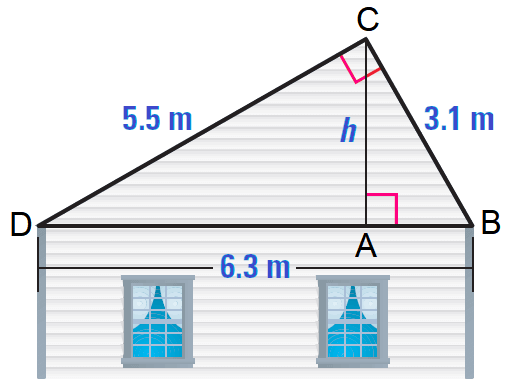
a.  Identify the similar triangles.

b.  Find the height h of the roof.

Solution (a) :

We may find it helpful to sketch the three similar right triangles so that the corresponding angles and sides have the same orientation. Mark the congruent angles.

Notice that some sides appear in more than one triangle.

For instance, BC is the hypotenuse in ΔBCA and the shorter leg in ΔBDC.

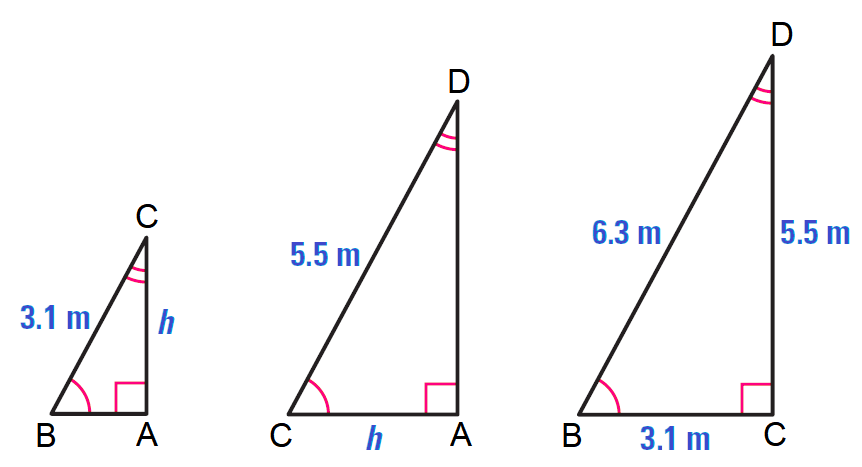
In the diagram shown above,

ΔBCA ∼ ΔCDA ∼ ΔBDC

Solution (b) :

Use the fact that ΔBCA ∼ ΔBDC to write a proportion.

Corresponding side lengths are in proportion :

CA/DC = BC/BD

Substitute.

h/5.5 = 3.1/6.3

Apply cross product property.

6.3h = 3.1 (5.5)

Solve for h.

h ≈ 2.7

Hence, the height of the roof is about 2.7 meters.

Using a Geometric Mean

Example 1 :

Find the value of x in the diagram shown below.

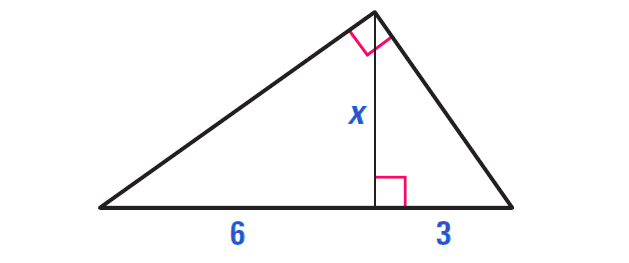
Solution :

Apply Geometric Mean Theorem 1.

x/3 = 6/x

Apply cross product property.

x² = 18

Solve for x.

x = √18

x = √(3 ⋅ 3 ⋅ 2)

x = 3√2

Example 2 :

Find the value of y in the diagram shown below.

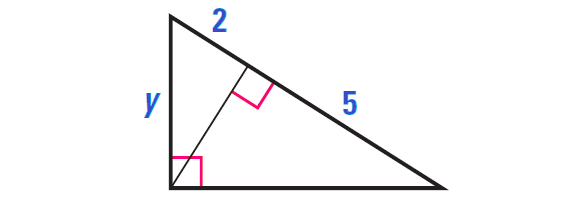
Solution :

Apply Geometric Mean Theorem 2.

y/2 = (5 + 2)/y

y/2 = 7/y

Apply cross product property.

y² = 14

Solve for x.

x = √14

Using Indirect Measurement

Example :

To estimate the height of a monorail track, your friend holds a cardboard square at eye level. Your friend lines up the top edge of the square with the track and the bottom edge with the ground. You measure the distance from the ground to your friend’s eye and the distance from your friend to the track.

In the diagram shown below, XY = h - 5.75 is the difference between the track height h and your friend’s eye level. Find the height of the track. 

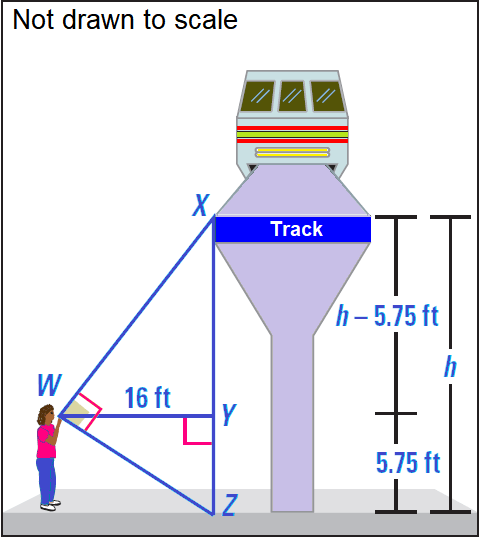
Solution :

Use Geometric Mean Theorem 2 to write a proportion involving XY. Then you can solve for h.

Geometric Mean Theorem 2 :

XY/WY = WY/ZY

Substitute.

(h - 5.75)/16 = 16/5.75

Apply cross product property.

5.75(h - 5.75) = 16²

Distributive property.

5.75h - 33.0625 = 256

Add 33.0625 to each side.

5.75h = 289.0625

Divide each side by 5.75.

h ≈ 50

Hence, the height of the track is about 50 feet.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.