SIMPLE AND COMPOUND INTEREST

Simple Interest

The formulas given below will be useful to solve problems on simple interest. 

I = Prt

A = I + P

A ----> Accumulated value (final value )  

P ----> Principal (initial value of an investment) 

r ----> Annual interest rate (in decimal)

I ----> Amount of interest 

t ----> Time (in years)

Compound Interest

The formulas given below will be useful to solve problems on compound interest.

A = P(1 + r/n)^nt

C.I = A - P

A -----> Accumulated value (final value )  

P -----> Principal (initial value of an investment) 

r -----> Annual interest rate (in decimal)

n -----> Number of times interest compounded per year

t -----> Time (in years)

C.I -----> Amount of interest

Difference between Simple Interest and Compound Interest

Important Note :

When we look at the above picture, it is clear that interest earned in S.I and C.I is same ($100) for the 1st year when interest is compounded annually in C.I.

Difference between Compound and Simple Interest for 2 Years and 3 Years

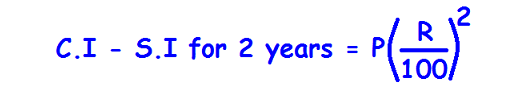
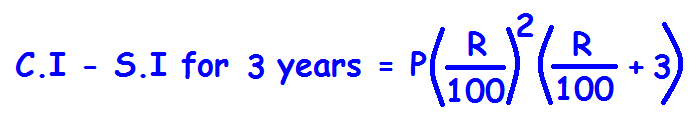
The above two formulas are applicable only in the following conditions.

1. The principal in simple interest and compound interest must be same.

2. Rate of interest must be same in simple interest and compound interest.

3. In compound interest, interest has to be compounded annually.

Solved Examples

Example 1 :

Find the simple interest for 2 years on $2000 at 6% per year.

Solution :

Formula for simple interest is

I  =  Pnr / 100 

Here, P = 2000, n = 2, r = 6

I  =  (2000 x 2 x 6) / 100

=  240

So, the interest earned is $240.

Example 2 :

In simple interest, a sum of money doubles itself in 10 years. Find the number of years it will take to triple itself. 

Solution :

Let P be the sum of money invested. 

Given : Sum of money doubles itself in 10 years

Then, P will become 2P in 10 years. 

Now we can calculate interest for ten years as given below 

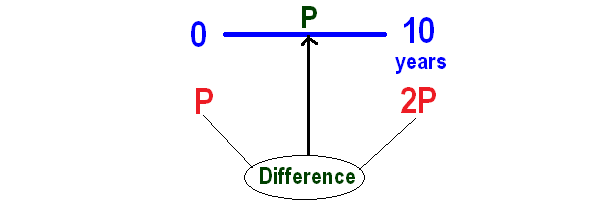
From the above calculation, P is the interest for the first 10 years. 

In simple interest, interest earned will be same for every year.

So, interest earned in the next 10 years also will be P. 

It has been explained below.

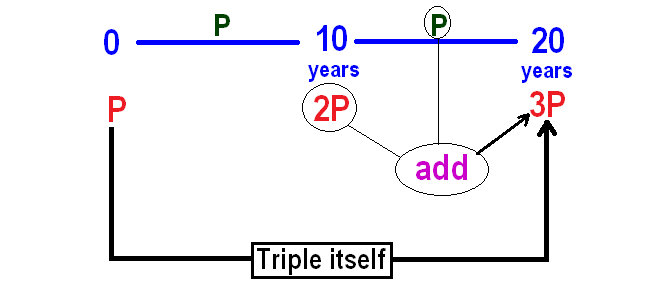
So, it will take 20 years for the principal to become triple itself.

Example 3 :

In simple interest, a sum of money amounts to $ 6200 in 2 years and $ 7400 in 3 years. Find the principal.

Solution :

At the end of 2 years, we get $6200

At the end of 3 years, we get $7400

From these two information, we can get the interest earned in the 3rd year as given below.

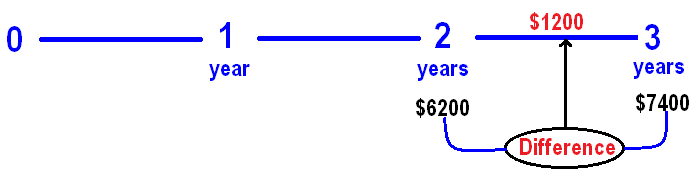
In simple interest, interest will be same for every year.

Based on this, we can calculate the principal as given below.

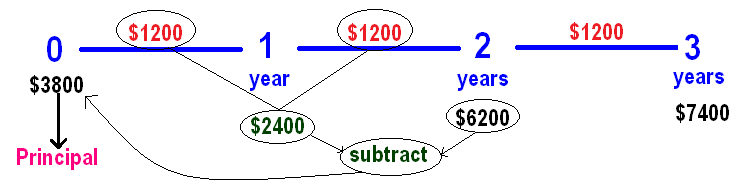
So, the principal is $3800.

Example 4 :

$800 is invested in  where the rate of interest is 20% per year. If interest is compounded half yearly, what will be the accumulated value and compound interest after 2 years ?

Solution :

The formula to find accumulated value is 

A  =  P(1 + r/n)^nt

A -----> Accumulated value (final value )  

P -----> Principal (initial value of an investment) 

r -----> Annual interest rate (in decimal)

n -----> Number of times interest compounded per year

t -----> Time (in years)

Here,

P  =  800

r  =   20%   =  0.2

n  =  2

t  =  2

Accumulated Value :

=  800(1 + 0.1)⁴

=  800(1.1)⁴

=  800 x 1.4641

=  1171.28

Compound Interest :

=  A - P 

=  1171.28 - 800

=  371.28

The accumulated value and compound interest after two years will be $1171.28 and $371.28 respectively.  

Example 5 :

A sum of money placed at compound interest doubles itself in 3 years. In how many years will it amount to four times itself ?

Solution :

Let P be the amount invested initially. 

From the given information, P becomes 2P in 3 years. 

Since the investment is in compound interest, the principal in the 4th year will be 2P 

And 2P becomes 4P (it doubles itself) in the next 3 years. 

Therefore, at the end of 6 years accumulated value will be 4P.

So, the amount deposited will amount to 4 times itself in 6 years.3

Example 6 :

The difference between the compound interest and simple interest on a certain investment at 10% per year for 2 years is $631. Find the value of the investment. 

Solution :

The difference between compound interest and simple interest for 2 years is 631.

Then we have,

P(R/100)²  =  631 

Substitute R = 10.

P(10/100)²  =  631 

=  631 

=  631 

Multiply both sides by 100 

P  =  631 x 100 

P  =  63100

So, the value of the investment is $63100.

Example 7 :

The difference between the compound interest and simple interest on a certain principal is at 10% per year for 3 years is $31. Find the principal. 

Solution :

The difference between compound interest and simple interest for three years is 31.

Then we have,

P(R/100)²(R/100 + 3)  =  31 

Substitute R = 10.

P(10/100)²(10/100 + 3)  =  31 

P(1/10)²(1/10 + 3)  =  31 

(31/10)

=  31 

Multiply both sides by 1000/31.

P  =  31 x (1000/31) 

P  =  1000

So, the principal is $1000.

Example 8 :

The compound interest and simple interest on a certain sum for 2 years is $ 1230 and $ 1200 respectively. The rate of interest is same for both compound interest and simple interest and it is compounded annually. What is the principal ?

Solution :

To find the principal, we need rate of interest. So, let us find the rate of interest first. 

Step 1 :

Simple interest for two years is $1200. So interest per year in simple interest is $600 

So, compound interest for 1st year is $600 and for 2nd year is $630.

(Since it is compounded annually, S.I and C.I for 1st year would be same) 

Step 2 : 

When we compare the compounded interest for 1st year and 2nd year, it is clear that the interest earned in 2nd year is 30 more than the first year. 

Because, in compound interest, interest $600 earned in 1st year earned this $30 in 2nd year. 

It can be considered as simple interest for one year.

That is principle  =  600, interest  =  30 

I  =  PRT / 100

30  =  (600 x R x 1) / 100

30  =  6R

Divide both sides by 6.

30/6  =  R 

5  =  R

So, R  =  5%

Step 3 : 

The difference between compound interest and simple interest for two years years is 

=  1230 - 1200

=  30

Then we have,

P(R/100)²  =  30 

Substitute R = 5. 

P(5/100)²  =  30 

P(1/20)²  =  30 

P(1/400)  =  30 

Multiply both sides by 400 

P  =  30 x 400 

P  =  12000

So, the principal is $12000.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.