SIMPLIFY RADICAL EXPRESSIONS

In this section, you will learn how to simplify radical expressions.

Like Radicals :

The radicals which are having same number inside the root and same index is called like radicals.

Unlike Radicals :

Unlike radicals don't have same number inside the radical sign or index may not be same.

We can add and subtract like radicals only.

Question 1 :

Simplify :

√20 - √225 + √80

Solution :

Decompose 20, 225 and 80 into prime factors using synthetic division. 

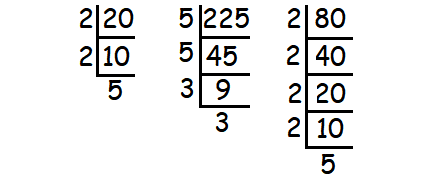
√20  =  √2 ⋅ 2 ⋅ 5  =  2√5

√225  =  √5 ⋅ 5 ⋅ 3 ⋅ 3  =  5 ⋅ 3  =  15

√225  =  √2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 5  =  (2 ⋅ 2)√5  =  4√5

Then, we have

√20 - √225 + √80  =  2√5 - 15 + 4√5

√20 - √225 + √80  =  6√5 - 15

√20 - √225 + √80  =  6√5 - 15

√20 - √225 + √80  =  3(2√5 - 5)

Question 2 :

Simplify :

√27 + √75 + √108 - √48

Solution :

Decompose 27, 75, 48 and 108 into prime factors using synthetic division. 

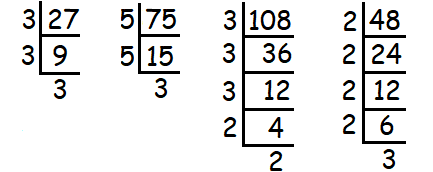
√27  =   √(3 ⋅ 3 ⋅ 3)  =  3√3

√75  =   √(5 ⋅ 5 ⋅ 3)  =  5√3

√108  =   √(3 ⋅ 3 ⋅ 3 ⋅ 2 ⋅ 2)  =  3 ⋅ 2 ⋅ √3  =  6√3

√48  =  √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 3)  =  2 ⋅ 2 ⋅ √3  =  4√3

Then, we have

√27 + √75 + √108 - √48  =   3√3 + 5√3 + 6√3 - 4√3

√27 + √75 + √108 - √48  =   10√3

Question 3 :

Simplify the following radical expression

5√28 - √28 + 8√28

Solution :

5√28 - √28 + 8 √28

Because all the terms in the above radical expression are like terms, we can simplify as given below. 

5√28 - √28 + 8√28  =  12√28

5√28 - √28 + 8√28  =  12√(2 ⋅ 2 ⋅ 7)

5√28 - √28 + 8√28  =  12 ⋅ 2√7

5√28 - √28 + 8√28  =  24√7

Question 4 :

Simplify the following radical expression

9√11 - 6√11 

Solution :

9√11 - 6√11 

Because the terms in the above radical expression are like terms, we can simplify as given below. 

9√11 - 6√11  =  3√11

Question 5 :

Simplify the following radical expression

7√8 - 6√12 - 5√32

Solution :

7√8 - 6√12 - 5√32

Decompose 8, 12 and 32 into prime factors.

7√8  =  7√(2 ⋅ 2 ⋅ 2)  =  7 ⋅ 2√2  =  14√2

6√12  =  6√(2 ⋅ 2 ⋅ 3)  =  6 ⋅ 2√3  =  12√3

5√32  =  √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2)  =  5 ⋅ 2 ⋅ 2 ⋅ √2  =  20√2

Then, we have

7√8 - 6√12 + 5√32  =  14√2 - 12√3 - 20√2

7√8 - 6√12 + 5√32  =  14√2 - 12√3 - 20√2

7√8 - 6√12 + 5√32  =  -6√2 - 12√3

7√8 - 6√12 + 5√32  =  -6(√2 + 2√3)

Question 6 :

Simplify the following radical expression

2√99 + 2√27 - 4√176 - 3√12

Solution :

Decompose 99, 27, 176 and 12 into prime factors.

2√99  =  2√(3 ⋅ 3 ⋅ 11)  =  2 ⋅ 3√11  =  6√11

2√27  =  2√(3 ⋅ 3 ⋅ 3)  =  2 ⋅ 3√3  =  6√3

4√176  =  √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 11)  =  4 ⋅ 2 ⋅ 2√11  =  16√11

3√12  =  3√(2 ⋅ 2 ⋅ 3)  =  3 ⋅ 2√3  =  6√3

Then, we have

2√99 + 2√27 - 4√176 - 3√12  =  6√11 + 6√3 - 16√11 - 6√3

2√99 + 2√27 - 4√176 - 3√12  =  -10√11

Question 7 :

Simplify the following radical expression

³√16 - ³√2 + 4³√54

Solution :

Decompose 16 and 54 into prime factors.

³√16  =  √(2 ⋅ 2 ⋅ 2 ⋅ 2)  =  2³√2

4³√54  =  4³√(3 ⋅ 3 ⋅ 3 ⋅ 2)  =  4(3³√2) = 12³√2

Then, we have

³√16 - ³√2 - 4³√54  =  2³√2 - ³√2 + 12³√2

³√16 + ³√2 - 4³√54  =  13³√2

Question 8 :

Simplify the following radical expression

³√24 + ³√375 - ³√3

Solution :

Decompose 24 and 375 into prime factors.

³√24  =  √(2 ⋅ 2 ⋅ 2 ⋅ 3)  =  2³√3

³√375  =  ³√(5 ⋅ 5 ⋅ 5 ⋅ 3)  =  5³√3

Then, we have

³√24 + ³√375 - ³√3 = 2³√3 + 5³√3 - ³√3

³√24 + ³√375 - ³√3 = 6³√3

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.