SIMPLIFYING EXPRESSIONS USING DISTRIBUTIVE PROPERTY

Expand and Simplify :

Example 1 :

4(x + 1) + 2(x + 2)

Solution :

Given, 4(x + 1) + 2(x + 2)

By using distributive property,

We get,

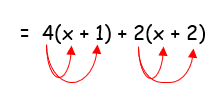
=  4x + 4 + 2x + 4

=  6x + 8

=  2(x + 4)

So, the answer is 2(x + 4)

Example 2 :

4(x + 2) + 2(x + 2)

Solution :

Given, 4(x + 2) + 2(x + 2)

By using distributive property,

We get,

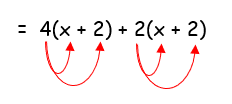
= 4x + 8 + 2x + 4

=  6x + 12

=  6(x + 2)

So, the answer is 6(x + 2)

Example 3 :

5(x - 1) + 2(x - 3)

Solution :

Given, 5(x - 1) + 2(x - 3)

By using distributive property,

we get,

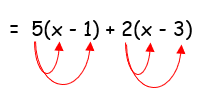
=  5x - 5 + 2x - 6

=  7x - 11

=  7x - 11

So, the answer is 7x - 11

Example 4 :

2(2x - 3) + 3(2 - x)

Solution :

Given, 2(2x - 3) + 3(2 - x)

By using distributive property,

we get,

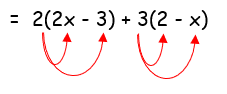
=  4x - 6 + 6 – 3x

=  x

So, the answer is x

Example 5 :

3(m + 2) - 2(m - 6) 

Solution :

Given, 3(m + 2) - 2(m - 6) 

By using distributive property,

we get,

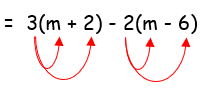
=  3m + 6 – 2m + 12

=  m + 18

So, the answer is m + 18

Example 6 :

2(m - 1) - 5(m + 2) 

Solution :

=  2(m - 1) - 5(m + 2)  

=  2m - 2 – 5m - 10

=  - 3m – 12

=  - 3(m + 4)

So, the answer is - 3(m + 4)

Example 7 :

2(x + 1) - 2(2x + 3) 

Solution :

=  2(x + 1) - 2(2x + 3)  

=  2x + 2 – 4x - 6

=  - 2x – 4

=  - 2(x + 2)

So, the answer is - 2(x + 2)

Example 8 :

8(2 + x) - (5x + 3) 

Solution :

=  8(2 + x) - (5x + 3) 

=  16 + 8x – 5x - 3

=  3x + 13

=  3x + 13

So, the answer is 3x + 13

Example 9 :

9(x - 2) + 3(7 – 4x)

Solution :

=  9(x - 2) + 3(7 – 4x)  

=  9x - 18 + 21 – 12x

=  - 3x + 3

=  - 3(x – 1)

So, the answer is - 3(x – 1)

Example 10 :

9(2 – 5x) - 2(3x + 2)

Solution :

=  9(2 – 5x) - 2(3x + 2)

  =  18 – 45x – 6x – 4

=  -51x + 14

=  -51x + 14

So, the answer is -51x + 14.

Example 11 :

- 4(2n – 3) - 3(3n - 5)

Solution :

=  - 4(2n – 3) - 3(3n - 5)  

=  - 8n + 12 – 9n + 15

=  - 17n + 27

=  - 17n + 27

So, the answer is – 17n + 27

Example 12 :

7(x – 1) + 2(2x + 3) – 11x

Solution :

Given, 7(x – 1) + 2(2x + 3) – 11x

By using distributive property,

we get,

=  7(x – 1) + 2(2x + 3) – 11x 

=  7x – 7 + 4x + 6 – 11x

=  11x – 1 – 11x

=  - 1

So, the answer is – 1.

Example 13 :

A plumber charges $70 for the first thirty minutes of each house call plus $4 for each additional minute that she works. The plumber Kemin $122 for her time. What amount of time, in minute did the plumber work ?

a)  43    b)  48   c) 58   d) 64

Solution :

Let x be the number of minutes she works.

$70 for the first minute and $4 for each additional minute.

70 + 4(x - 30)

Plumber Kemin charges = $122x

70 + 4(x - 30) = 122

70 + 4x - 120 = 122

-50 + 4x = 122

4x = 122 + 50

4x = 172

x = 172/4

x = 43

So, the required number of minutes is 43.

Example 14 :

Gerg pays a fee of $20 a month for local calls. Long distance rates 6 cent per minute for in state calls and 5 cent per minute for out of state calls. Suppose Gerg makes 300 minutes of long distance phone calls in January and m of those minute are for in state calls.

i) Find an expression for Gerg's phone bill for January

ii)  Evaluate the expression to find the cost it Gerg had 37 minutes of in state calls in January.

Solution :

i)  The bill is the sum of monthly fee, in state charges and the out of  state charges.

If m = number of minutes of in state calls

300 - m = number of minutes out of state calls 

Let B be phone bill for the month of January.

B = 20 + m(0.06) + (300 - m) 0.05

= 20 + 0.06m + 15 - 0.05m

= 35 + 0.01m

So, the required expression is 35 + 0.01m

ii) Evaluate the expression when m = 37

= 35 + 0.01(37)

= 35 + 0. 37

= $35.37

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.