SIMPLIFYING EXPRESSIONS

To simplify algebraic expressions, we need to the combine like terms. 

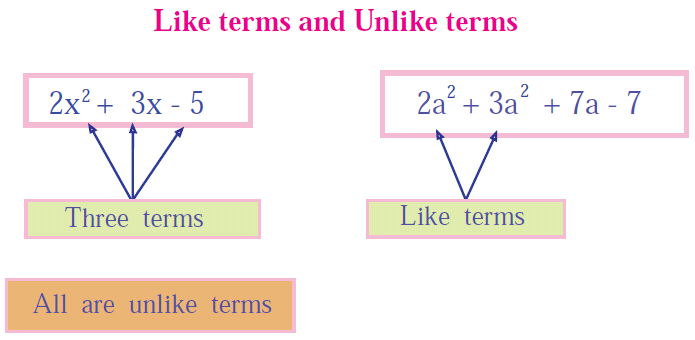
Before we do combining like terms, first let us come to know what like terms and unlike terms are. 

Like Terms or Similar Terms: 

Like terms are the terms which have the same variables with same exponent for each variable.

Example :

7x, 3x, - 4x

Unlike Terms or Dissimilar Terms: 

Unlike terms are the terms which have same variables or different variables. 

If they have same variables, the exponents will not be same. 

Example :

9x², 5xy, - 4xy², y, 6

More clearly, 

Solved Examples

Example 1:

Simplify :

7(x - 3) + 2(2x - 5) - 3(x - 5)

Solution:

=  7(x - 3) + 2(2x - 5) - 3(x - 5)

Use distributive property. 

=  7(x) + 7(-3) + 2(2x) + 2(-5) - 3(x) - 3(-5)

=  7x - 21 + 4x - 10 - 3x + 15

Combine the like terms. 

=  8x - 16

Example 2 :

Simplify :

4x - (2 + 4x) - 2(x - 1) - 8(x -3)

Solution :

  =  4x - (2 + 4x) - 2(x - 1) - 8(x -3)

Use distributive property. 

=  4x - 2 - 4x - 2(x) - 2(-1) - 8(x) - 8(-3)

=  4x - 2 - 4x - 2x + 2 - 8x + 24

Combine the like terms. 

=  10x + 24

Example 3 :

Simplify : 

(2x - 7)/5 + (x + 9)/15 - (2x -2)/5

Solution :

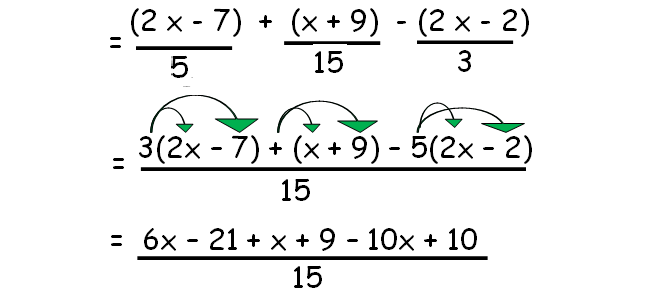
Combine the like terms.

=  (-3x - 2) / 15

Example 4 :

Simplify : 

(3x + 41)/2 + (x - 3)/5 - (9 - 2x)/6

Solution :

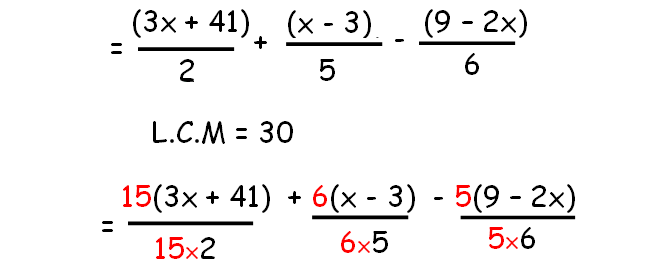
Use distributive property and combine the like terms. 

Example 5 :

Simplify : 

(9n⁴)^1/2

Solution :

=  (9n⁴)^1/2

=  (3² ⋅ n⁴)^1/2

=  (3²)^1/2 ⋅ (n⁴)^1/2

=  3^{2 ⋅ 1/2} ⋅ n^{4 ⋅ 1/2}

=  3¹ ⋅ n²

=  3 ⋅ n²

=  3n²

Example 6 :

Simplify : 

(8x³y⁶)^1/3

Solution :

=  (8x³y⁶)^1/3

=  (2³ ⋅ x³ ⋅ y⁶)^1/3

=  (2³)^1/3 ⋅ (x³)^1/3 ⋅ (y⁶)^1/3 

=  2^{3 ⋅ 1/3} ⋅ x^{3 ⋅ 1/3} ⋅ y^{6 ⋅ 1/3} 

=  2¹ ⋅ x¹ ⋅ y²

=  2xy²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.