SIMPLIFYING RADICAL EXPRESSIONS INVOLVING FRACTIONS

Quotient Property of Radicals

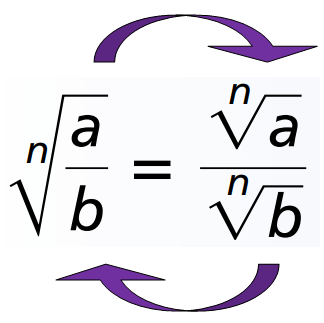
Step 1 :

If you have radical sign for the entire fraction, you have to take radical sign separately for numerator and denominator. 

Step 2 :

We have to simplify the radical term according to its power.

• If you have square root (√), you have to take one term out of the square root for every two same terms multiplied inside the radical.
• If you have cube root (³√), you have to take one term out of cube root for every three same terms multiplied inside the radical.
• If you have fourth root (⁴√), you have to take one term out of fourth root for every four same terms multiplied inside the radical.

Note : 

In case, you have prime number inside the radical sign in denominator, you have to multiply both numerator and denominator by the prime number along with the radical sign.

Step 3 :

After taking the terms out from radical sign, we have to simplify the fraction.

Solved Examples

Example 1 :

Use the quotient property to write the following radical expression in simplified form. 

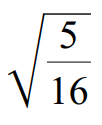
Solution :

√(5/16)  =  √5 / √16

√(5/16)  =  √5 / √(4 ⋅ 4)

Index of the given radical is 2.

Because its index is 2, we can take one term out of radical for every two same terms multiplied inside the radical sign.

√(5/16)  =  √5 / 4

Example 2 :

Use the quotient property to write the following radical expression in simplified form. 

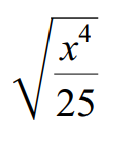
Solution :

√(x⁴/25)  =  √x⁴ / √25

√(x⁴/25)  =  √(x² ⋅ x²) / √(5 ⋅ 5)

Index of the given radical is 2.

Because its index is 2, we can take one term out of radical for every two same terms multiplied inside the radical sign.

√(x⁴/25)  =  x² / 5

Example 3 :

Use the quotient property to write the following radical expression in simplified form. 

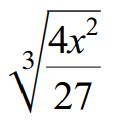
Solution :

³√(4x²/27)  =  ³√4x² / ³√27

³√(4x²/27)  =  ³√(4x²) / ³√(3 ⋅ 3 ⋅ 3)

Index of the given radical is 3. 

Because its index is 3, we can one term out of radical for every three same terms multiplied inside the radical sign.

³√(4x²/27)  =  ³√(4x²) / 3

Example 4 :

Use the quotient property to write the following radical expression in simplified form. 

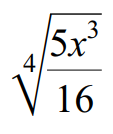
Solution :

⁴√(5x³/16)  =  ⁴√(5x³) / ⁴√16

⁴√(5x³/16)  =  ⁴√5x³ / ⁴√(2 ⋅ 2  ⋅ 2 ⋅ 2)

Index of the given radical is 4.

Because its index is 4, we can take one term out of the radical for every four same terms multiplied inside the radical sign. 

⁴√(5x³/16)  =  ⁴√5x³ / 2

Example 5 :

Use the quotient property to write the following radical expression in simplified form. 

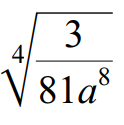
Solution :

⁴√(3/81a⁸)  =  ⁴√3 / ⁴√(81a⁸)

⁴√(3/81a⁸)  =  ⁴√3 / ⁴√(3a² ⋅ 3a² ⋅ 3a² ⋅ 3a²) 

Index of the given radical is 4.

Because its index is 4, we can take one term out of the radical for every four same terms multiplied inside the radical sign. 

⁴√(3/81a⁸)  =  ⁴√3 / 3a²

Example 6 :

Use the quotient property to write the following radical expression in simplified form. 

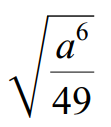
Solution :

√(a⁶/49)  =  √a⁶/√49

√(a⁶/49)  =  √(a³ ⋅ a³)/(7 ⋅ 7)

Index of the given radical is 2.

Because its index is 2, we can take one term out of the radical for every two same terms multiplied inside the radical sign. 

√(a⁶/49)  =  a³/7

Example 7 :

Use the quotient property to write the following radical expression in simplified form. 

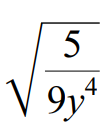
Solution :

√(5/9y⁴)  =  √5 / √9y⁴

√(5/9y⁴)  =  √5 / (3y² ⋅ 3y²)

Index of the given radical is 2.

Because its index is 2, we can take one term out of the radical for every two same terms multiplied inside the radical sign. 

√(5/9y⁴)  =  √5 / 3y²

Example 8 :

Use the quotient property to write the following radical expression in simplified form. 

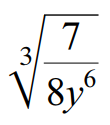
Solution :

³√(7/8y⁶)  =  ³√7 / ³√(8y⁶)

³√(7/8y⁶)  =  ³√7 / ³√(2y² ⋅ 2y² ⋅ 2y²)

Index of the given radical is 3.

Because its index is 3, we can take one term out of the radical for every three same terms multiplied inside the radical sign. 

³√(7/8y⁶)  =  ³√7 / 2y²

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.