SIMPLIFYING RADICAL EXPRESSIONS
The following steps will be useful to simplify any radical expressions.
Step 1 :
Decompose the number inside the radical into prime factors.
Step 2 :
If you have square root (√), you have to take one term out of the square root for every two same terms multiplied inside the radical.
Step 3 :
If you have cube root (3√), you have to take one term out of cube root for every three same terms multiplied inside the radical.
Step 4 :
If you have fourth root (4√), you have to take one term out of fourth root for every four same terms multiplied inside the radical.
Step 5 :
Combine the radical terms using mathematical operations.
Example :
√18 + √8 = √(3 ⋅ 3 ⋅ 2) + √(2 ⋅ 2 ⋅ 2)
√18 + √8 = 3√2 + 2√2
√18 + √8 = 5√2
Solved Examples
Example 1 :
Simplify the radical expression :
√169 + √121
Solution :
Decompose 169 and 121 into prime factors using synthetic division.
|
√169 = √(13 ⋅ 13) √169 = 13 |
√121 = √(11 ⋅ 11) √121 = 11 |
So, we have
√169 + √121 = 13 + 11
√169 + √121 = 24
Example 2 :
Simplify the radical expression :
√20 + √320
Solution :
Decompose 20 and 320 into prime factors using synthetic division.
|
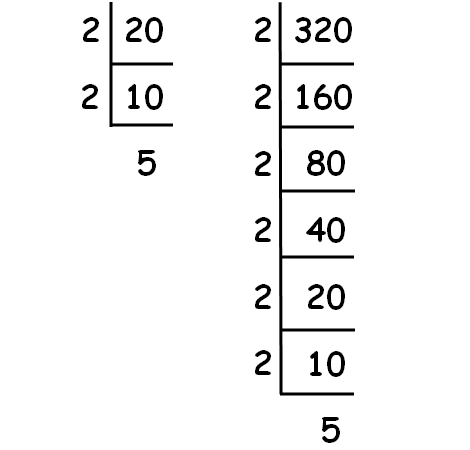
√20 = √(2 ⋅ 2 ⋅ 5) √20 = 2√5 |
√320 = √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 5) √320 = 2 ⋅ 2 ⋅ 2 ⋅ √5 √320 = 8√5 |
So, we have
√20 + √320 = 2√5 + 8√5
√20 + √320 = 10√5
Example 3 :
Simplify the radical expression :
√117 - √52
Solution :
Decompose 117 and 52 into prime factors using synthetic division.
|
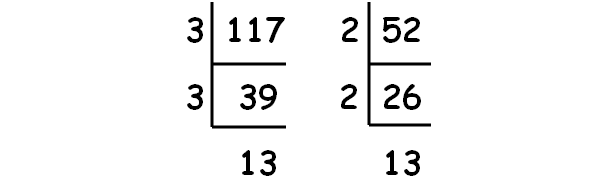
√117 = √(3 ⋅ 3 ⋅ 13) √117 = 3√13 |
√52 = √(2 ⋅ 2 ⋅ 13) √52 = 2√13 |
So, we have
√117 - √52 = 3√13 - 2√13
√117 + √52 = √13
Example 4 :
Simplify the radical expression :
√243 - 5√12 + √27
Solution :
Decompose 243, 12 and 27 into prime factors using synthetic division.
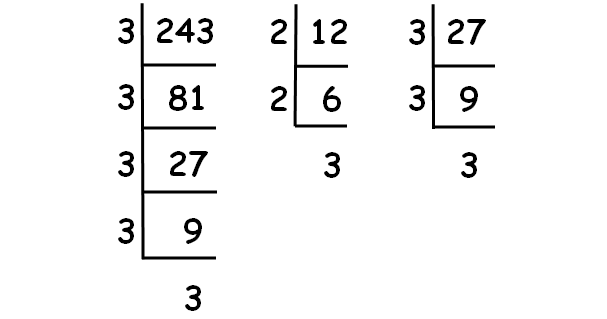
√243 = √(3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3) = 9√3
√12 = √(2 ⋅ 2 ⋅ 3) = 2√3
√27 = √(3 ⋅ 3 ⋅ 3) = 3√3
So, we have
√243 - 5√12 + √27 = 9√3 - 5(2√3) + 3√3
Simplify.
√243 - 5√12 + √27 = 9√3 - 10√3 + 3√3
√243 - 5√12 + √27 = 2√3
Example 5 :
Simplify the radical expression :
-√147 - √243
Solution :
Decompose 147 and 243 into prime factors using synthetic division.
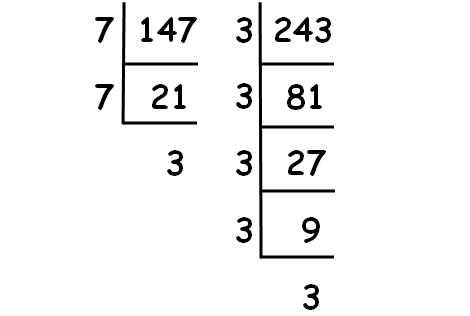
√147 = √(7 ⋅ 7 ⋅ 3) = 7√3
√243 = √(3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3) = 9√3
So, we have
-√147 - √243 = -7√3 - 9√3
-√147 - √243 = -16√3
Example 6 :
Simplify the radical expression :
(√13)(√26)
Solution :
Decompose 13 and 26 into prime factors.
13 is a prime number. So, it can't be decomposed anymore.
√26 = √(2 ⋅ 13) = √2 ⋅ √13
So, we have
(√13)(√26) = (√13)(√2 ⋅ √13)
(√13)(√26) = (√13 ⋅ √13)√2
(√13)(√26) = 13√2
Example 7 :
Simplify the radical expression :
(3√14)(√35)
Solution :
Decompose 14 and 35 into prime factors.
√14 = √(2 ⋅ 7) = √2 ⋅ √7
√35 = √(5 ⋅ 7) = √5 ⋅ √7
So, we have
(3√14)(√35) = 3( √2 ⋅ √7)(√5 ⋅ √7)
(3√14)(√35) = 3(√7 ⋅ √7)(√2 ⋅ √5)
(3√14)(√35) = 3(7)√(2 ⋅ 5)
(3√14)(√35) = 21√10
Example 8 :
Simplify the radical expression :
(8√117) ÷ (2√52)
Solution :
Decompose 117 and 52 into prime factors using synthetic division.
|
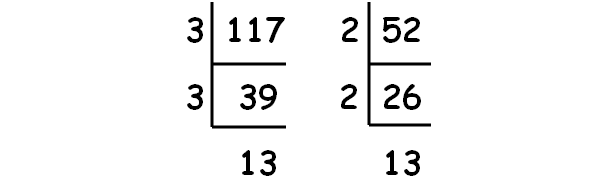
√117 = √(3 ⋅ 3 ⋅ 13) √117 = 3√13 |
√52 = √(2 ⋅ 2 ⋅ 13) √52 = 2√13 |
(8√117) ÷ (2√52) = 8(3√13) ÷ 2(2√13)
(8√117) ÷ (2√52) = 24√13 ÷ 4√13
(8√117) ÷ (2√52) = 24√13 / 4√13
(8√117) ÷ (2√52) = 6
Example 9 :
Simplify the radical expression :
(8√3)2
Solution :
(8√3)2 = 8√3 ⋅ 8√3
(8√3)2 = (8 ⋅ 8)(√3 ⋅ √3)
(8√3)2 = (64)(3)
(8√3)2 = 192
Example 10 :
Simplify the radical expression :
(√2)3 + √8
Solution :
(√2)3 + √8 = (√2 ⋅ √2 ⋅ √2) + √(2⋅ 2 ⋅ 2)
(√2)3 + √8 = (2 ⋅ √2) + 2√2
(√2)3 + √8 = 2√2 + 2√2
(√2)3 + √8 = 4√2
Example 11 :
Simplify :
4√(x4/16)
Solution :
4√(x4/16) = 4√(x4) / 4√16
4√(x4/16) = 4√(x ⋅ x ⋅ x ⋅ x) / 4√(2 ⋅ 2 ⋅ 2 ⋅ 2)
4√(x4/16) = x / 2
Example 12 :
Simplify :
3√(125p6q3)
Solution :
3√(125p6q3) = 3√(5 ⋅ 5 ⋅ 5 ⋅ p2 ⋅ p2 ⋅ p2 ⋅ q ⋅ q ⋅ q)
3√(125p6q3) = 5p2q
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
If you have any feedback about our math content, please mail us :
v4formath@gmail.com
We always appreciate your feedback.
You can also visit the following web pages on different stuff in math.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Trigonometry word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Recent Articles
-
Practice Test in Subtracting Decimals
Oct 21, 20 01:35 AM
Practice Test in Subtracting Decimals
-
Subtraction Worksheet with Answers
Oct 21, 20 01:04 AM
Subtraction Worksheet with Answers
-
Powers of Monomials
Oct 20, 20 09:11 PM
Powers of Monomials
