SKETCH A GRAPH FROM A VERBAL DESCRIPTION

Use the information below to sketch a graph of the polynomial function y  =  f(x). 

* f(x) is positive on the intervals (-2, -1) and (1, 2).

* f(x) is negative on the intervals (-∞, -2), (-1, 1) and (2, ∞).

* f(x) is increasing on the intervals (-∞, -1.5) and (0, 1.5).

* f(x) is decreasing on the intervals (-1.5, 0) and (1.5, ∞)

Step 1 :

Using the x-values in positive and negative intervals, we can draw vertical lines parallel to y-axis as shown below. 

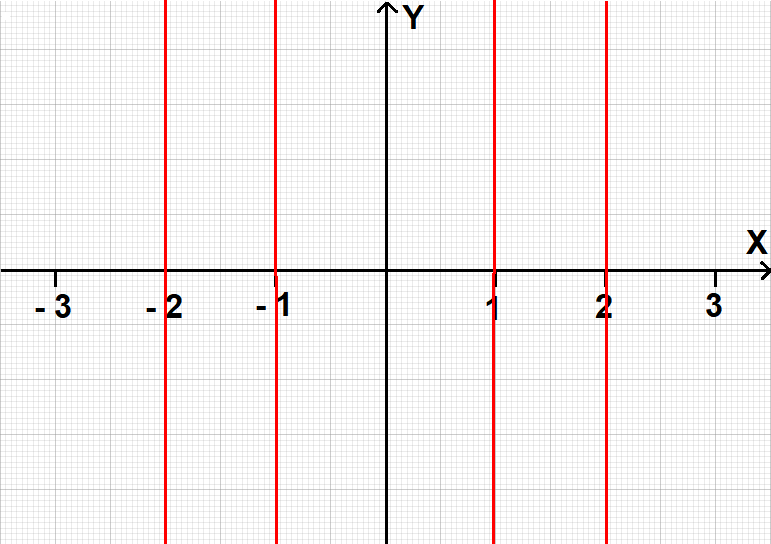
Step 2 :

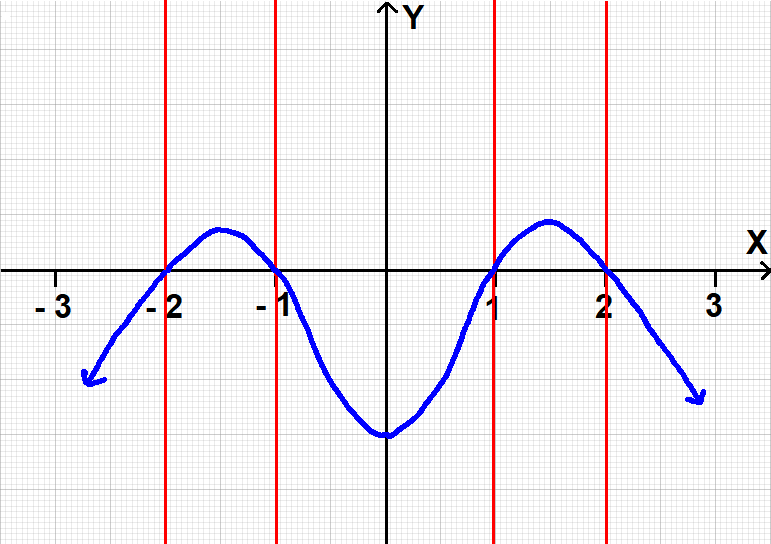
The x-intercepts of the graph are

(-2, 0), (-1, 0), (1, 0) and (2, 0)

That is, the graph has to intersect x-axis at the above points. 

Step 3 : 

f(x) is positive on the intervals (-2, -1) and (1, 2).

So, the graph should be above the x-axis on the intervals

(-2, -1) and (1, 2). 

Step 4 : 

f(x) is negative on the intervals (-∞, -2), (-1, 1) and (2, ∞).

So, the graph should be below the x-axis on the intervals

(-∞, -2), (-1, 1) and (2, ∞)

Step 5 : 

f(x) is increasing on the intervals (-∞, -1.5) and (0, 1.5).

When we look at the graph from left to right, the graph should be upward on the intervals

(-∞, -1.5) and (0, 1.5)

Step 6 : 

f(x) is decreasing on the intervals (-1.5, 0) and (1.5, ∞)

When we look at the graph from left to right, the graph should be downward on the intervals 

(-1.5, 0) and (1.5, ∞)

Try Yourself : 

Use the information below to sketch a graph of the polynomial function y  =  f(x). 

* f(x) is positive on the intervals (-4, -2) and (2, 4).

* f(x) is negative on the intervals (-∞, -4), (-2, 2) and (4, ∞).

* f(x) is increasing on the intervals (-∞, -3) and (0, 3).

* f(x) is decreasing on the intervals (-3, 0) and (3, ∞).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.