SKETCH AN ANGLE IN STANDARD POSITION IF TERMINAL ARM PASSES THROUGH A POINT
Example 1 :
Sketch an angle in standard position so that the terminal arm passes through each point.
(a) (2, 6)
Solution :
First let us plot the point (2, 6) in the graph paper.
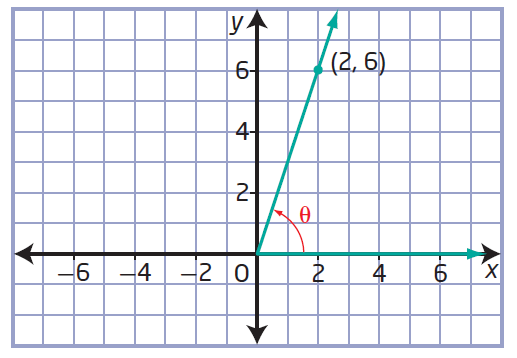
(b) (-4, 2)
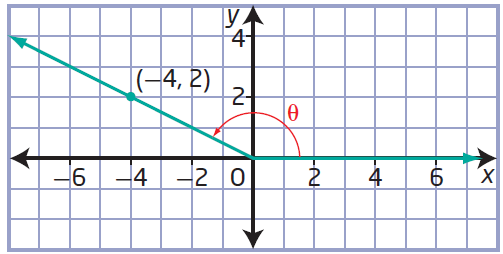
(c) (-5, -2)
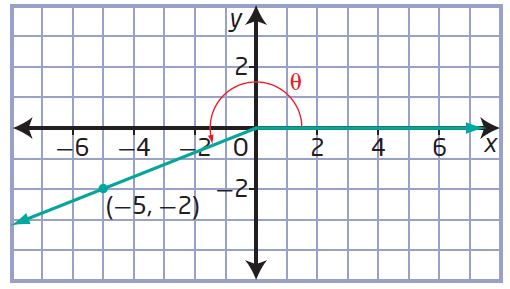
(d) (-1, 0)
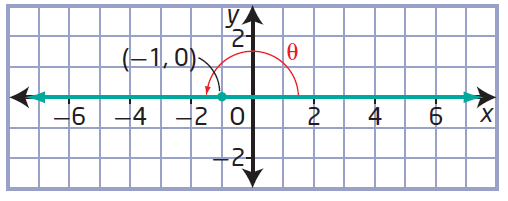
Example 2 :
Determine the exact values of the sine, cosine, and tangent ratios for each angle
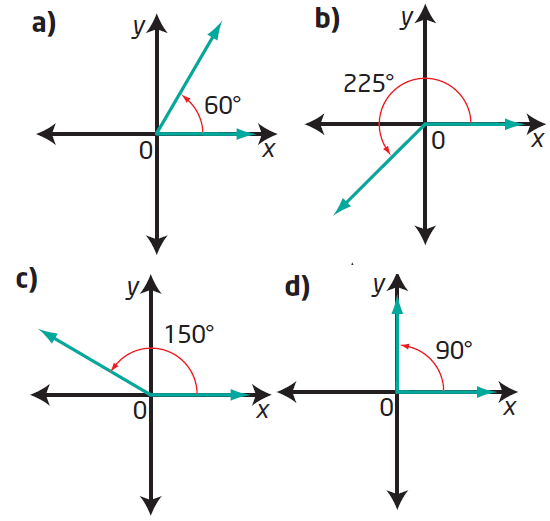
Solution :
By drawing a perpendicular line from A, we get a triangle OAB.
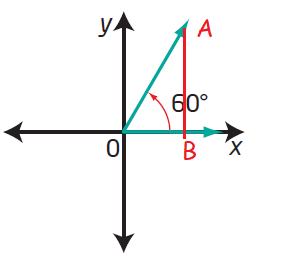
In triangle OAB,
OA = Hypotenuse side
OB = Adjacent side and AB = Opposite side
|
sin 60 = √3/2 |
cos 60 = 1/2 |
tan 60 = √3 |
Since the terminal arm lies in first quadrant, we have to take positive sign for sin 60.
(ii)
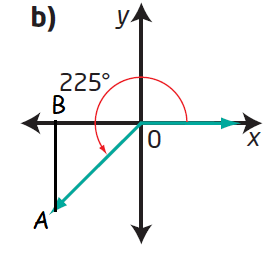
By drawing a perpendicular line from A, we get a triangle OAB.
In triangle OAB,
<BOA = 180 + θ
180 + θ = 225
θ = 225 - 180 = 45
Since the terminal arm lies in the 3rd quadrant, we have to use positive sign for tan and cot only.
|
sin 225 = -1/√2 |
cos 225 = -1/√2 |
tan 225 = 1 |
(iii)
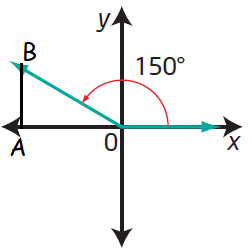
By drawing a perpendicular line from A, we get a triangle OAB.
In triangle OAB,
<AOB = 180 - θ
<AOB = 180 - 150
<AOB = 30
|
sin 150 = 1/2 |
cos 150 = -√3/2 |
tan 150 = -1/√3 |
(iv)
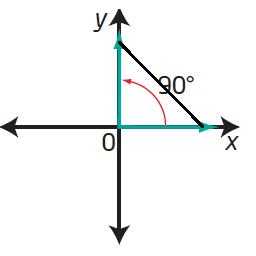
|
sin 90 = 1 |
cos 90 = 0 |
tan 90 = undefined |
Example 3 :
The coordinates of a point P on the terminal arm of each angle are shown. Write the exact trigonometric ratios sin θ, cos θ, and tan θ for each.
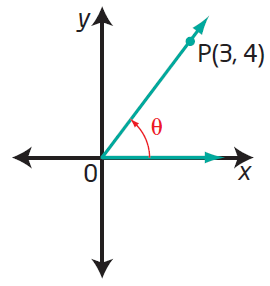
Solution :
Since the terminal arm lies in 3rd quadrant, we have to take positive signs for all trigonometric ratios.
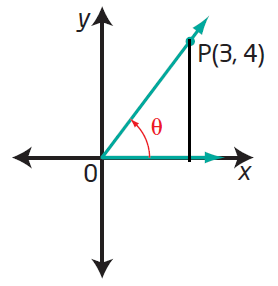 |
Horizontal length = 3 Vertical length = 4 Hypotenuse = √32 + 42 Hypotenuse = 5 sin θ = 4/5 cos θ = 3/5 tan θ = 4/3 |
(ii)
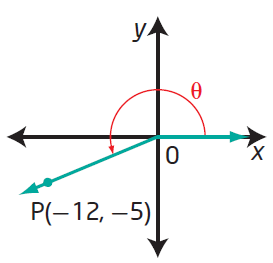
Since the terminal arm lies in 3rd quadrant, we have to take positive sign only for tan and cot.
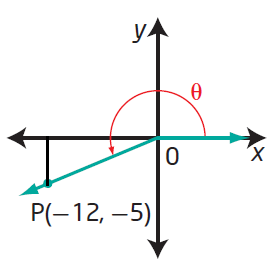 |
Horizontal length = 12 Vertical length = 5 Hypotenuse = √122 + 52 Hypotenuse = 13 sin θ = -5/13 cos θ = -12/13 tan θ = 5/12 |
(iii)
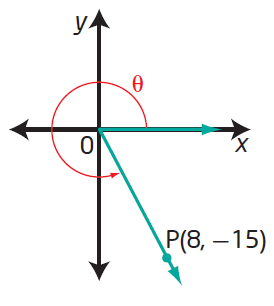
Since the terminal arm lies in 4th quadrant, we have to take positive sign only for cos and sec.
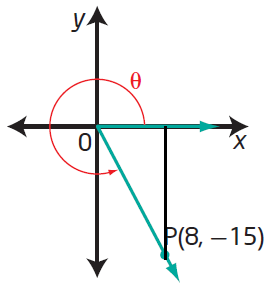 |
Horizontal length = 8 Vertical length = 15 Hypotenuse = √82 + 152 Hypotenuse = 17 sin θ = -15/17 cos θ = 8/17 tan θ = -15/8 |

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 150)
Apr 25, 25 11:46 AM
Digital SAT Math Problems and Solutions (Part - 150) -
AP Calculus AB Problems with Solutions (Part - 19)
Apr 24, 25 11:10 PM
AP Calculus AB Problems with Solutions (Part - 19) -
AP Calculus AB Problems with Solutions (Part - 18)
Apr 24, 25 11:06 PM
AP Calculus AB Problems with Solutions (Part - 18)
