SKETCHING A TRIANGLE AND DETERMINE THE MEASURE OF INDICATED SIDE

Sketch each triangle. Determine the measure of the indicated side.

Example 1 :

In triangle ABC, ∠A = 57°, ∠B = 73°, and AB = 24 cm. Find the length of AC.

Solution :

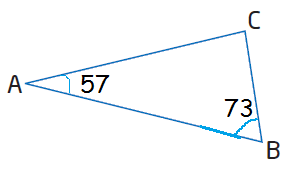
AB  =  c  =  24 cm, BC  =  a, AC  =  b, <A  =  57 and <B  =  73

In triangle ABC,

<A + <B + <C  =  180

57 + 73 + <C  =  180

<C  =  180 - 130  =  50

Using sin formula,

a/sin A  =  b/sin B  =  c/sin C

a/sin 57  =  b/sin 73  =  24/sin 50

We have to solve for b.

Equating 1 and 3, we get

b/sin 73  =  24/sin 50

b/0.9563   =  24/0.7660

b  =  31.33(0.9563)

b  =  29.96

b  =  30 cm (approximately)

Hence the indicated side is 30 cm.

Example 2 :

In triangle ABC, ∠B = 38°, ∠C = 56°, and BC = 63 cm. Find the length of AB.

Solution :

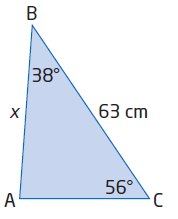
AB  =  c, BC  =  a = 63, AC  =  b, <C  =  56 and <B  =  38

In triangle ABC,

<A + <B + <C  =  180

<A + 38 + 56  =  180

<A  =  180 - 94  =  86

Using sin formula,

a/sin A  =  b/sin B  =  c/sin C

63/sin 86  =  b/sin 38  =  c/sin 56

We have to solve for c.

Equating 1 and 3, we get

63/sin 86  =  c/sin 56

63/0.9975   =  c/0.8290

63.15  =  c/0.8290

c  =  63.15(0.8290)

c  =  52.35

c  =  52.4 cm (approximately)

Hence the indicated side is 52.4 cm.

Example 3 :

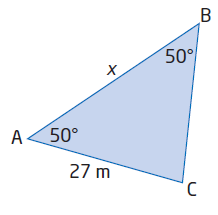
In triangle ABC, ∠A = 50°, ∠B = 50°, and AC = 27 m. Find the length of AB.

Solution :

AB  =  c, BC  =  a = 27 m,  AC  =  b = 27 m, <A  =  50 and <B  =  50

In triangle ABC,

<A + <B + <C  =  180

50 + 50 + <C  =  180

<C  =  180 - 100  =  80

Using sin formula,

a/sin A  =  b/sin B  =  c/sin C

27/sin 50  =  27/sin 50  =  c/sin 80

We have to solve for c.

Equating 1 and 3, we get

27/sin 50  =  c/sin 80

27/0.7660   =  c/0.9848

35.24  =  c/0.9848

c  = 35.24(0.9848)

c  =  34.70 m

Hence the indicated side is 34.7 m.

Apart from the stuff given above, if you need any other stuff, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.