SKETCHING RATIONAL FUNCTIONS

Sketch the graphs of the following functions.

Problem 1 :

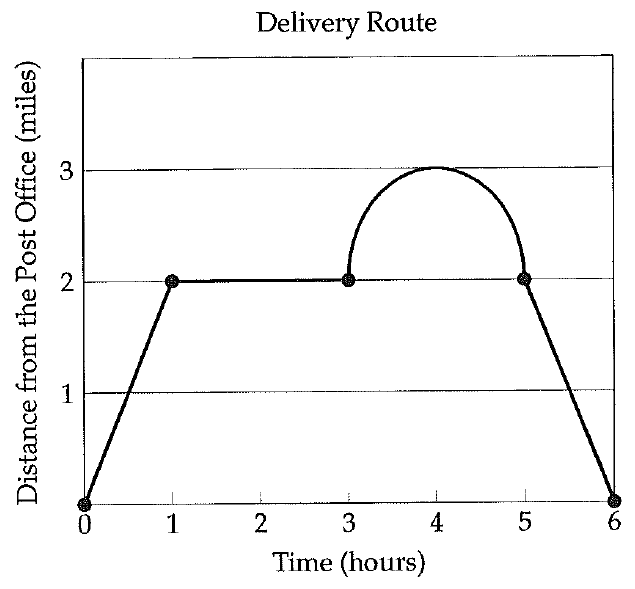
y  =  (x²+1)/(x²-4)

Solution :

Domain and range :

Possible values of x are R - {-2, 2} ==>  Domain

y values are R - {0} ==>  Range

Intercepts :

To find x intercept, put y  =  0

(x²+1)/(x²-4)  =  0

Since there is no real values of x, it will not intersect on x-axis.

y-intercept :

Put x  =  0

y  =  -1/4

Critical points :

f(x)  =  (x²+1)/(x²-4)

u  =  x² + 1 and v  =  x²-4

u'  =  2x and v'  =  2x

f'(x)  =  [2x(x²-4) - 2x(x²+1)] / (x²-4)²

f'(x)  =  [2x³-8x - 2x³-2x] / (x²-4)²

f'(x)  =  -10x / (x²-4)²

f'(x)  =  0

-10x  =  0

x  =  0

Plotting these points on the number line and dividing into intervals, we get (-∞, 0) and (0, ∞).

Local extrema :

f'(x)  =  -10x / (x²-4)²

u  =  -10x and v  =  (x²-4)²

u'  =  -10 and v'  =  4x(x²-4)

f''(x)  =  [-10(x²-4)²+40x²(x²-4)] /(x²-4)⁴

f''(x)  =  -10(x²-4)[(x²-4)+4x²] /(x²-4)⁴

f''(x)  =  -10(x²-4)(5x²-4) /(x²-4)⁴

f''(0)  =  -  < 0 (Maximum)

Maximum  point :

When x  =  0

y  =  (x²+1)/(x²-4)

y  =  -1/4

So, the maximum point is (0, -0.25)

Intervals of concavity :

f''(x)  =  -10(x²-4)(5x²-4) /(x²-4)⁴

f''(x)  =  0

(x²-4)(5x²-4)  =  0

Point of inflection :

f(x)  =  (x²+1)/(x²-4)

When x  =  2 and -2, y approaches ∞. Let us find asymptotes to get the graph more clearly.

Asymptotes :

Horizontal asymptote :

Degree of numerator  =  degree of denominator

y  =  leading coefficient of numerator/leading coefficient of denominator

y  =  1/1  ==>  1

Vertical asymptote :

x²-4  =  0

x  =  2, -2

Problem 2 :

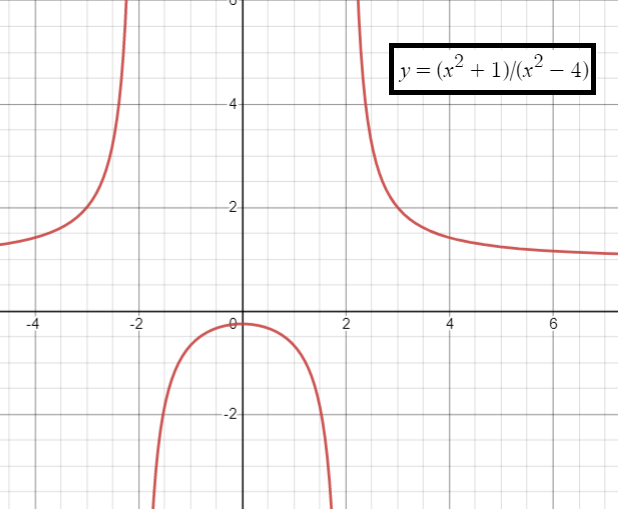
y  =  1/(1+e^-x)

Solution :

The function is defined for all real values of x.

So, domain is all real values and range is (0, 1).

Intercepts :

When x  =  0, y  =  1/2

So, y-intercept is (0, 1/2).

Critical points :

f'(x)  =  [(1+e^-x) (0) - 1(-e^-x)]/(1+e^-x)²

f'(x)  =  1(e^-x)/(1+e^-x)²

f'(x)  =  0

e^-x/(1+e^-x)²  =  0

e^-x  =  0

Which is not possible, so there is no maximum.

Asymptotes :

No vertical asymptote. From the domain, we know vertical asymptotes are y = 0 and y  =  1.

Problem 3 :

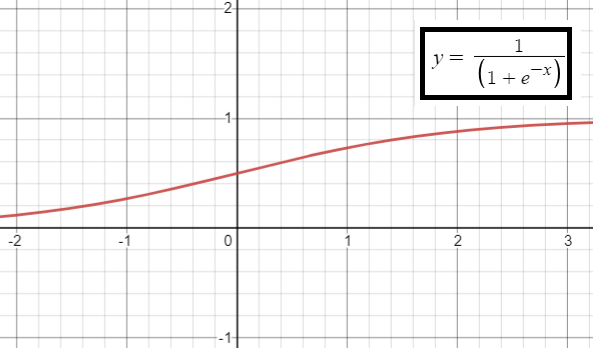
y  =  x³/24 - log x

Solution :

y  =  x³/24 - log x

Domain :

y is defined only for positive values.

Intercepts :

There is no intercepts.

Critical points :

f'(x)  =  3x²/24 - 1/x

f'(x)  =  x²/8 - 1/x

f'(x)  =  0

x²/8 - 1/x  =  0

x²/8 = 1/x

x  =  2

Local extrema :

f''(x)  =  2x/8 + 1/x²

f''(x)  =  x/4 + 1/x²

f''(2)  =  2/4 + 1/2²

=  1/2 + 1/4

=  3/4 > 0 (minimum)

Minimum point :

f(2)  =  2³/24 - log 2

f(2)  =  1/3 - log 2

From here, range is  1/3 - log 2 > ∞.

Point of inflection :

There is no point of inflection.

There is no horizontal asymptotes. Vertical asymptote is y  =  0.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.