SLANT ASYMPTOTE WORKSHEET

Find the slant or oblique asymptote :

1. f(x) = 1/(x + 6)

2. f(x) = (x² + 2x - 3)/(x² - 5x + 6)

3. f(x) = (x² + 3x + 2)/(x - 2)

1. Answer :

f(x) = 1/(x + 6)

Step 1 :

In the given rational function, the largest exponent of the numerator is 0 and the largest exponent of the denominator is 1.

Step 2 :

Clearly, the largest exponent of the numerator is less than the largest exponent of the denominator.

So, there is no slant asymptote.

2. Answer :

f(x) = (x² + 2x - 3)/(x² - 5x + 6)

Step 1 :

In the given rational function, the largest exponent of the numerator is 2 and the largest exponent of the denominator is 2.

Step 2 :

Clearly, the largest exponents  of the numerator and the denominator are equal.

So, there is no slant asymptote.

3. Answer :

f(x) = (x² + 3x + 2)/(x - 2)

Step 1 :

In the given rational function, the largest exponent of the numerator is 2 and the largest exponent of the denominator is 1.

Step 2 :

Clearly, the largest exponent of the numerator is greater than the largest exponent of the denominator by one. So, there is a slant asymptote.

Step 3 :

To get the equation of the slant asymptote, we have to divide the numerator by the denominator using long division as given below.

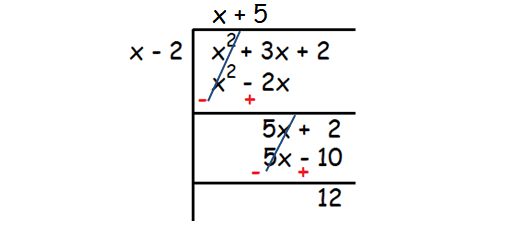
In the above long division, the quotient is (x + 5).

So, the equation of the slant asymptote is

y = x + 5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.