SLOPE AND GRAPHING REVIEW

Slope intercept form is y = m x + b, where m is slope and b is the y-intercept. We can use this form of a linear equation to draw the graph of that equation on the x-y coordinate plane.

There are many ways to draw a graph for a line. This is one of the methods in graphing a line. In this method we can graph a line using slope and y-intercept.

Let us see some example problems to understand the method.

Example 1 :

Draw the graph of the following line using slope intercept

x - 2y = 6

Solution :

x - 2y = 6

To find slope and y-intercept at a time, we have to convert the given equation to the slope intercept form.

Subtract x on both sides.

x - x - 2y = 6 - x

-2y = -x + 6

divide the equation by (-2) 

-2y/(-2) = -x/(-2) + 6/(-2)

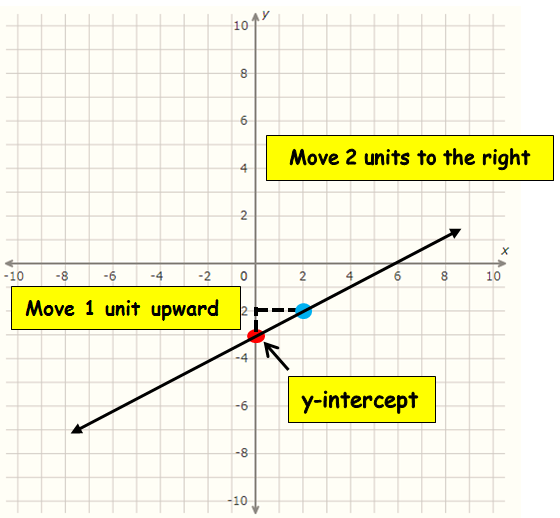
y = (1/2) x - 3

Comparing this equation with slope intercept form

y = m x + b

We get slope (m) as 1/2 and y-intercept -3

slope = change of y/change in x

Example 2 :

Draw the graph of the following line using slope intercept

y = -x - 4

Solution :

The given equation exactly matches the slope intercept form

Comparing this equation with slope intercept form

y = m x + b

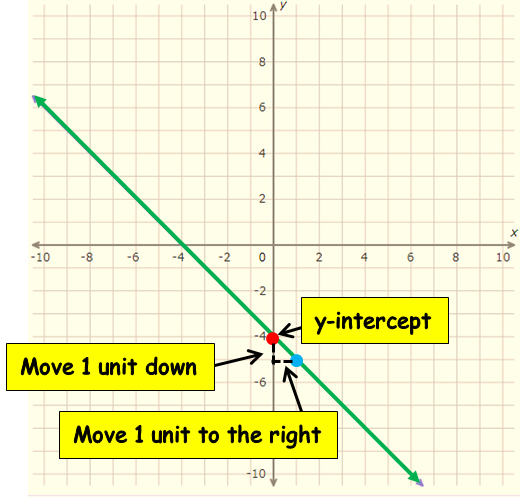
We get slope (m) as -1 and y-intercept -4

slope = change of y/change in x  => -1/1

Example 3 :

Draw the graph of the following line using slope intercept

x + 3y = 6

Solution :

Now we have to subtract x on both sides

x - x  + 3y = 6 - x 

3y = 6 - x 

divide by 3 on both sides

y = 6/3 - x/3

y = 2 - x/3

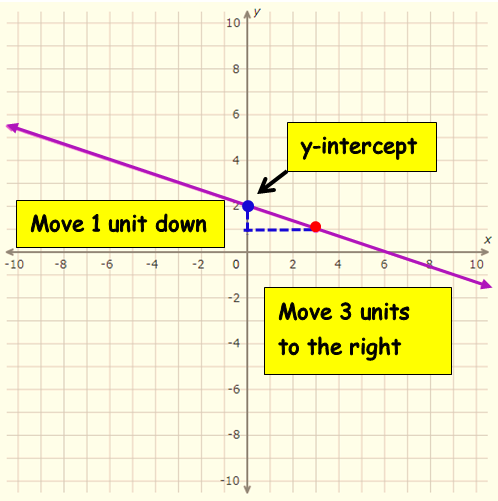
y = (-1/3) x + 2

Comparing this equation with slope intercept form

y = m x + b

We get slope (m) as -1/3 and y-intercept 2

slope = change of y/change in x  => -1/3

Example 4 :

Draw the graph of the following line using slope and y intercept

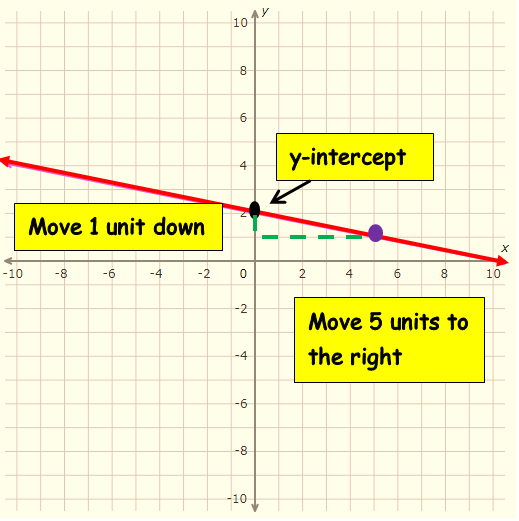
y = (-1/5)x + 2

Solution :

The given equation exactly matches the slope intercept form.

Comparing this equation with slope intercept form

y = m x + b

We get slope (m) as -1/5 and y-intercept 2

slope = change of y/change in x  => -1/5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.