SLOPE INTERCEPT FORM WORKSHEET

Problem 1 :

Graph the line with slope -2 and y-intercept 4.

Problems 2-5 : Write the equation that describes each line in slope-intercept form.

Problem 2 :

Slope = 2/5, y-intercept = 6. 

Problem 3 :

Slope = 0, y-intercept = -4. 

Problem 4 :

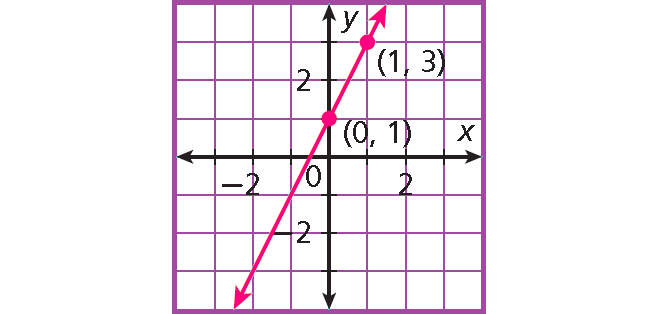
Problem 5 :

Slope = 4, (2, 5) is on the line.

Problems 6-8 : Write each equation in slope-intercept form. Then graph the line described by the equation.

Problem 6 :

4x - y - 3  =  0

Problem 7 :

2x + 3y - 6  =  0

Problem 8 :

3x + 2y  =  8

Problem 9 :

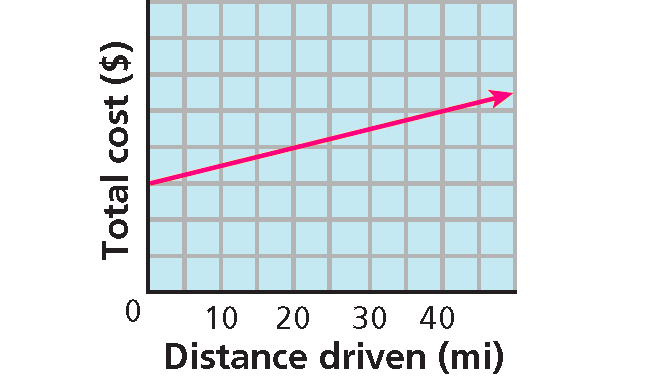
To rent a vehicle, a moving company charges $30.00 plus $0.50 per mile. The cost as a function of the number of miles driven is shown in the graph.

Problem 10 :

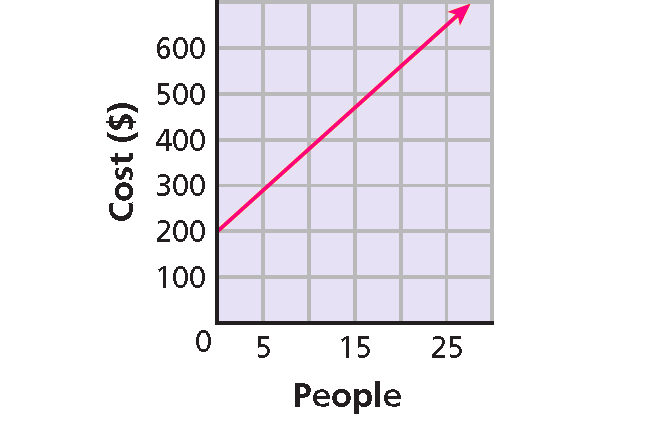
A caterer charges a $200 fee plus $18 per person served. The cost as a function of the number of guests is shown in the graph.

Answers

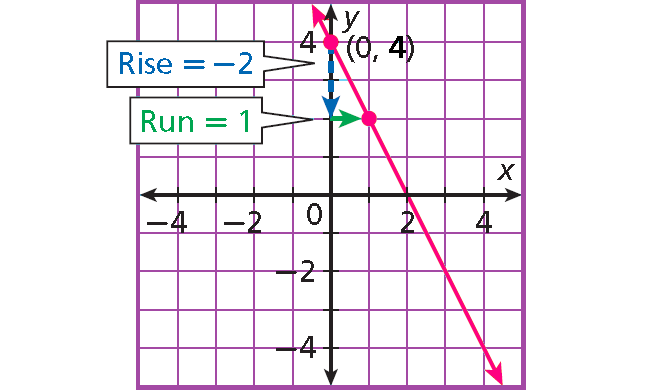
1. Answer :

Step 1 : 

The y-intercept is 4, so the line contains (0, 4). Plot (0, 4).

Step 2 : 

Slope  =  change in y / change in x  =  -2/1

Count 2 units down and 1 unit right from (0, 4) and plot another point.

Step 3 : 

Draw the line through the two points.

2. Answer :

Write the slope-intercept form equation of a line : 

y  =  mx + b

Substitute 2/5 for m and 6 for b. 

y  =  (2/5)x + 6

y  =  2x/5 + 6

3. Answer :

Write the slope-intercept form equation of a line : 

y  =  mx + b

Substitute 0 for m and -4 for b. 

y  =  (0)x + (-4)

y  =  0 - 4

y  =  -4

4. Answer :

Step 1 : 

Find the y-intercept.

The graph crosses the y-axis at (0, 1), so b = 1.

Step 2 : 

Find the slope.

The line contains the points (0, 1) and (1, 3).

Use the slope formula. 

m  =  (y₂ - y₁) / (x₂ - x₁)

Substitute (0, 1) for (x₁ , y₁) and (1, 3) for (x₂ , y₂).

m  =  (3 - 1) / (1 - 0)

m  =  2/1

m  =  2

Step 3 : 

Write the slope-intercept form equation of a line : 

y  =  mx + b

Substitute 2 for m and 1 for b.

y  =  2x + 1

5. Answer :

Step 1 :

Find the y-intercept.

Write the slope-intercept form equation of a line : 

y  =  mx + b

Substitute 4 for m, 2 for x, and 5 for y.

5  =  4(2) + b

5  =  8 + b

Subtract 8 from each side.

-3  =  b

Step 2 : 

Write the slope-intercept form equation of a line : 

y  =  mx + b

Substitute 4 for m and -3 for b.

y  =  4x + (-3)

y  =  4x - 3

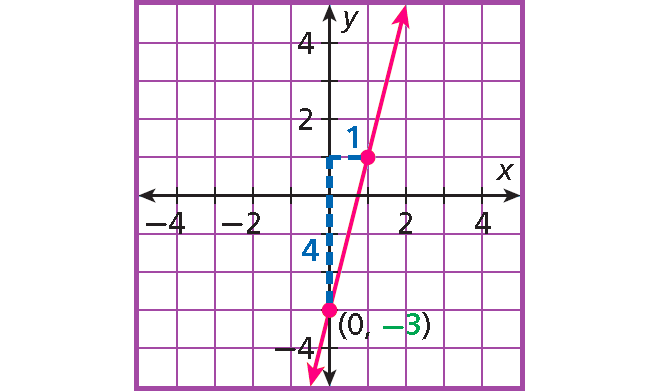
6. Answer :

Step 1 :

Write the given equation slope-intercept form : 

4x - y - 3  =  0

Add y to each side. 

4x - 3  =  y

y  =  4x - 3

y = 4x - 3 is in the form y = mx + b. 

Slope : m  =  4  =  4/1

y-intercept : b  =  -3

Step 2 : 

Plot (0, -3). 

Step 3 : 

Count 4 units up and 1 unit right and plot another point. 

Step 4 : 

Draw the line connecting the two points.

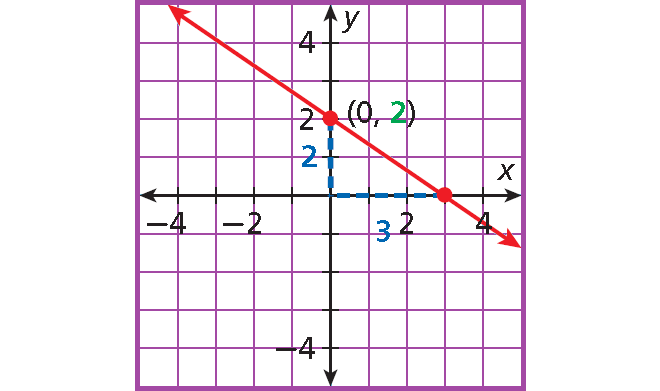
7. Answer :

Step 1 :

Write the given equation slope-intercept form : 

2x + 3y - 6  =  0

Subtract 2x from each side and add 6 to each side.  

3y  =  -2x + 6

Divide each side 3.

3y/3  =  (-2x + 6)/3

y  =  -2x/3 + 6/3

y  =  (-2/3)x + 2

Slope : m  =  -2/3

y-intercept : b  =  2

Step 2 : 

Plot (0, 2). 

Step 3 : 

Count 2 units down and 3 unit right and plot another point. 

Step 4 : 

Draw the line connecting the two points.

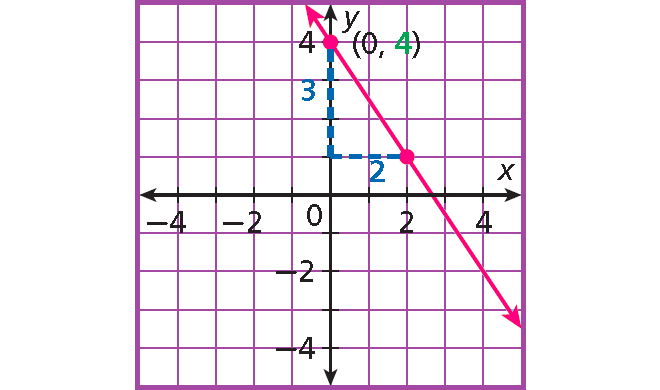
8. Answer :

Step 1 :

Write the given equation slope-intercept form : 

3x + 2y  =  8

Subtract 3x from each side and add 6 to each side.  

2y  =  -3x + 8

Divide each side 2.

2y/2  =  (-3x + 8)/2

y  =  -3x/2 + 8/2

y  =  (-3/2)x + 4

Slope : m  =  -3/2

y-intercept : b  =  4

Step 2 : 

Plot (0, 4). 

Step 3 : 

Count 3 units down and 2 unit right and plot another point. 

Step 4 : 

Draw the line connecting the two points.

9. Answer :

Part (i) : 

Cost is $0.50 per mile times miles plus $30.00.

y  =  0.50x + 30

An equation is y = 0.5x + 30.

Part (ii) : 

The y-intercept is 30. This is the cost for 0 miles, or the initial fee of $30.00. 

The slope is 0.5.

This is the rate of change of the cost : $0.50 per mile.

Part (iii) : 

y  =  0.5x + 30

Substitute 150 for x in the equation.

=  0.5(150) + 30

=  75 + 30

=  105

The cost of the vehicle for 150 miles is $105.

10. Answer :

Part (i) : 

Cost is $18 per guest plus $200.

y  =  18x + 200

An equation is y = 18x + 200.

Part (ii) : 

The y-intercept is 200. This is the cost for 0 guests, or the initial fee of $200. 

The slope is 18.

This is the rate of change of the cost : $18 per guest.

Part (iii) : 

y  =  18x + 50

Substitute 200 for x in the equation.

=  18(200) + 200

=  3600 + 200

=  3800

The cost of catering for 200 guests is $3800.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.