SLOPE INTERCEPT FORM

You can graph a straight line using its slope and the point that contains the y-intercept.

Graphing by Using Slope and y-intercept

Example 1 :

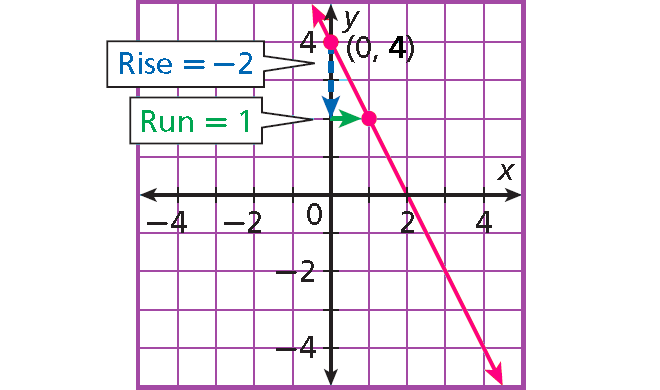
Graph the line with slope -2 and y-intercept 4.

Solution :

Step 1 :

The y-intercept is 4, so the line contains (0, 4). Plot (0, 4).

Step 2 :

Count 2 units down and 1 unit right from (0, 4) and plot another point.

Step 3 : 

Draw the line through the two points.

Slope-Intercept Form of a Linear Equation

If a line has slope m and the y-intercept is b, then the line is described by the equation

y = m x + b

Any linear equation can be written in slope-intercept form by solving for y and simplifying.

In this form, you can immediately see the slope and y-intercept. Also, you can quickly graph a line when the equation is written in slope-intercept form.

Writing Linear Equations in Slope-Intercept Form

Write the equation that describes each line in slope-intercept form.

Example 2 : 

Slope = ⅖, y-intercept = 6. 

Solution :

Write the slope-intercept form equation of a line : 

y = mx + b

Substitute 2/5 for m and 6 for b. 

y = (⅖)x + 6

y = ²ˣ⁄₅ + 6

Example 3 : 

Slope = 0, y-intercept = -4. 

Solution :

Write the slope-intercept form equation of a line : 

y = mx + b

Substitute 0 for m and -4 for b. 

y = (0)x + (-4)

y = 0 - 4

y = -4

Example 4 : 

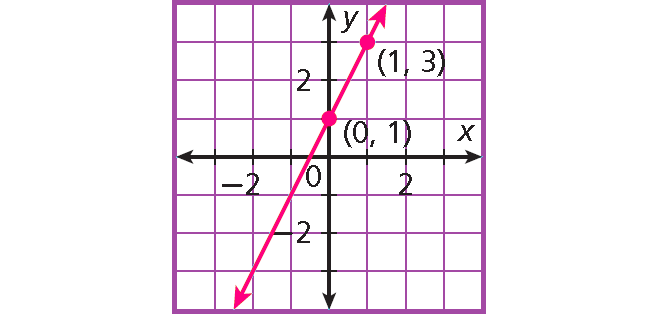
Solution :

Step 1 : 

Find the y-intercept.

The graph crosses the y-axis at (0, 1), so b = 1.

Step 2 : 

Find the slope.

The line contains the points (0, 1) and (1, 3).

Use the slope formula. 

Substitute (x₁ , y₁) = (0, 1) and (x₂ , y₂) = (1, 3).

m = ⁽³ ⁻ ¹⁾⁄₍₁ ₋ ₀₎

m = ²⁄₁

m = 2

Step 3 : 

Write the slope-intercept form equation of a line : 

y = mx + b

Substitute 2 for m and 1 for b.

y = 2x + 1

Example 5 : 

Slope = 4, (2, 5) is on the line.

Solution :

Step 1 :

Find the y-intercept.

Write the slope-intercept form equation of a line : 

y = mx + b

Substitute 4 for m, 2 for x, and 5 for y.

5 = 4(2) + b

5 = 8 + b

Subtract 8 from each side.

-3 = b

Step 2 : 

Write the slope-intercept form equation of a line : 

y = mx + b

Substitute 4 for m and -3 for b.

y = 4x + (-3)

y = 4x - 3

Using Slope-Intercept Form to Graph

Write each equation in slope-intercept form. Then graph the line described by the equation.

Example 6 : 

4x - y - 3 = 0

Solution :

Step 1 :

Write the given equation slope-intercept form : 

4x - y - 3 = 0

Add y to each side. 

4x - 3 = y

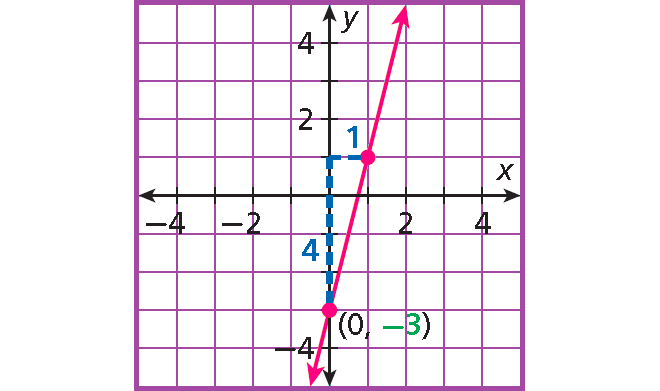
y = 4x - 3

y = 4x - 3 is in the form y = mx + b. 

Slope : m = 4 = ⁴⁄₁

y-intercept : b = -3

Step 2 : 

Plot (0, -3). 

Step 3 : 

Count 4 units up and 1 unit right and plot another point. 

Step 4 : 

Draw the line connecting the two points.

Example 7 : 

2x + 3y - 6 = 0

Solution :

Step 1 :

Write the given equation slope-intercept form : 

2x + 3y - 6 = 0

Subtract 2x from each side and add 6 to each side.  

3y = -2x + 6

Divide each side 3.

³ʸ⁄₃ = ⁽⁻²ˣ ⁺ ⁶⁾⁄₃

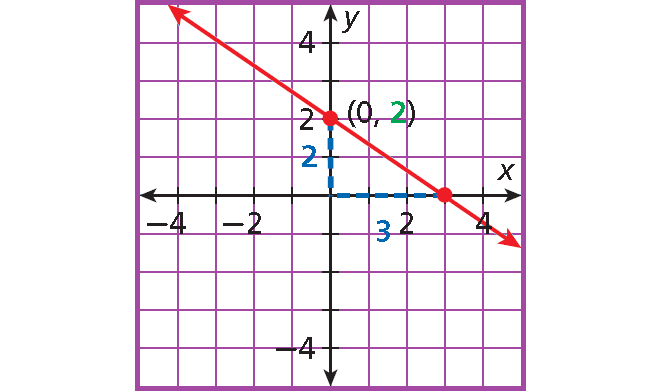
y = ⁻²ˣ⁄₃ + ⁶⁄₃

y = (⁻²⁄₃)x + 2

Slope : m = ⁻²⁄₃

y-intercept : b = 2

Step 2 : 

Plot (0, 2). 

Step 3 : 

Count 2 units down and 3 unit right and plot another point. 

Step 4 : 

Draw the line connecting the two points.

Example 8 : 

3x + 2y = 8

Solution :

Step 1 :

Write the given equation slope-intercept form : 

3x + 2y = 8

Subtract 3x from each side and add 6 to each side.  

2y = -3x + 8

Divide each side 2.

²ʸ⁄₂ = ⁽⁻³ˣ ⁺ ⁸⁾⁄₂

y = ⁻³ˣ⁄₂ + ⁸⁄₂

y = (⁻³⁄₂)x + 4

Slope : m = ⁻³⁄₂

y-intercept : b = 4

Step 2 : 

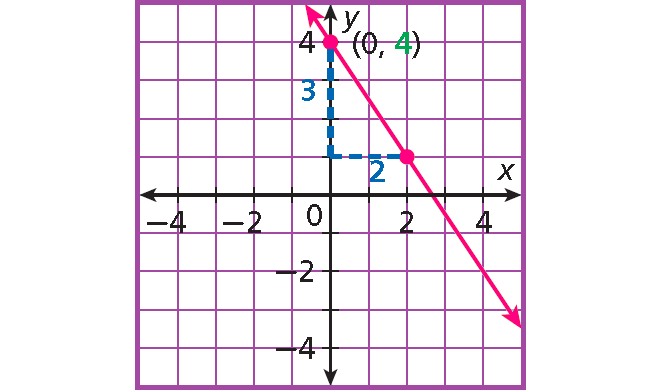
Plot (0, 4). 

Step 3 : 

Count 3 units down and 2 unit right and plot another point. 

Step 4 : 

Draw the line connecting the two points.

Consumer Application

Example 9 :

To rent a vehicle, a moving company charges $30.00 plus $0.50 per mile. The cost as a function of the number of miles driven is shown in the graph.

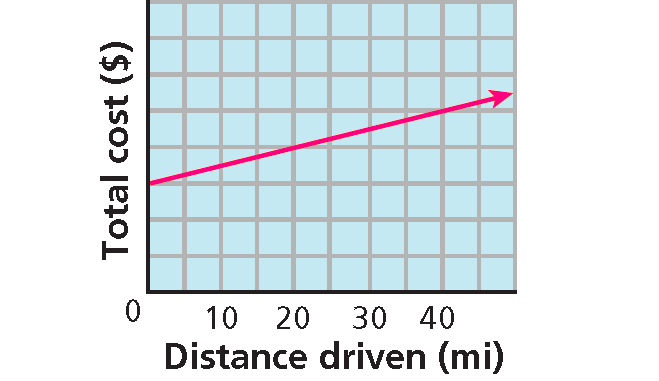
(i) Write an equation that represents the cost as a function of the number of miles.

(ii) Identify the slope and y-intercept and describe their meanings.

(iii) Find the cost of the van for 150 miles.

Solution :

Part (i) : 

Cost is $0.50 per mile times miles plus $30.00.

y = 0.50x + 30

An equation is y = 0.5x + 30.

Part (ii) : 

The y-intercept is 30. This is the cost for 0 miles, or the initial fee of $30.00. 

The slope is 0.5.

This is the rate of change of the cost : $0.50 per mile.

Part (iii) : 

y = 0.5x + 30

Substitute 150 for x in the equation.

y = 0.5(150) + 30

y = 75 + 30

y = 105

The cost of the vehicle for 150 miles is $105.

Example 10 : 

A caterer charges a $200 fee plus $18 per person served. The cost as a function of the number of guests is shown in the graph.

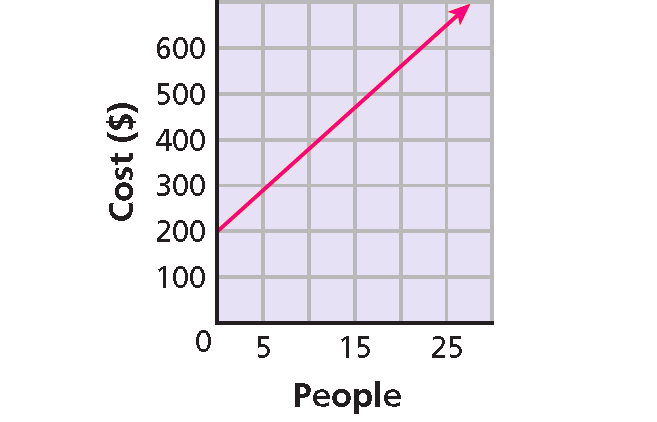
(i) Write an equation that represents the cost as a function of the number of guests.

(ii) Identify the slope and y-intercept and describe their meanings.

(iii) Find the cost of catering an event for 200 guests.

Solution :

Part (i) : 

Cost is $18 per guest plus $200.

y = 18x + 200

An equation is y = 18x + 200.

Part (ii) : 

The y-intercept is 200. This is the cost for 0 guests, or the initial fee of $200. 

The slope is 18.

This is the rate of change of the cost : $18 per guest.

Part (iii) : 

y = 18x + 50

Substitute 200 for x in the equation.

= 18(200) + 200

= 3600 + 200

= 3800

The cost of catering for 200 guests is $3800.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.