SLOPES OF HORIZONTAL AND VERTICAL LINES WORKSHEET

Find the slope of each line.

Problem 1 : 

Problem 2 : 

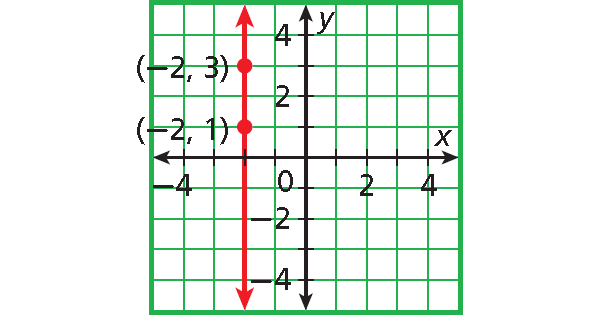
Problem 3 : 

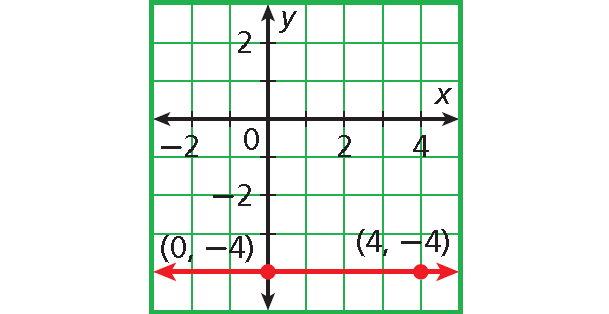
Problem 4 : 

Problem 5 :

Which of the following equations represents a vertical line that passes through the point (5, -3) ?

a)  y = -3      b)  y = -3x + 5   c)  x = 5       d) y = 5x - 3

Problem 6 :

The equation of a vertical line passing through the point (-4, 5) 

Problem 7 : 

The equation of a horizontal line passing through the point (3, 2).

Problem 8 : 

Sketch the region bounded by the three lines whose equations are given below. Label each with its equation. Find the area of the triangular region enclosed by the lines. You may want to use your calculator to create a table of values of the first line or simply use facts about the slope and y-intercept.

y = 2x - 4, x = -1 and y = 2

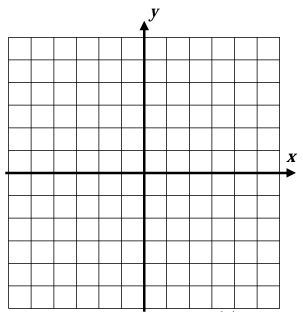
Problem 9 :

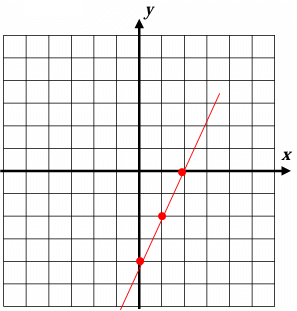
For each of the following, give the equation of the line shown.

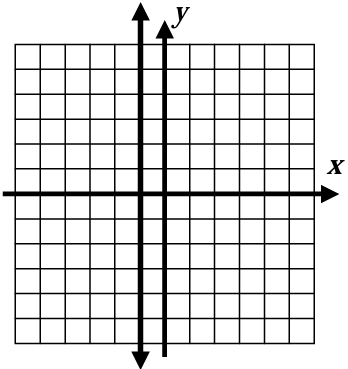
Problem 10 :

Problem 11 :

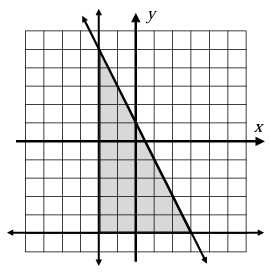
The triangular region shown below is bordered by one vertical line, one horizontal line, and one slanted line. State the equation of each line and determine the triangle’s area.

Detailed Answer Key

1. Answer : 

Slope :

=  rise / run 

=  (2 - 2)/[3 - (-1)]

=  0/(3 + 1)

=  0/4

=  0

The slope is 0. 

2. Answer : 

Slope :

=  rise / run 

=  (1 - 3)/[-2 - (-2)]

=  -2/(-2 + 2)

=  -2/0

=  undefined

The slope is undefined. 

3. Answer : 

Slope :

=  rise / run 

=  [-4 - (-4))/(4 - 0)

=  (-4 + 4)/4

=  0/4

=  0

The slope is 0. 

4. Answer : 

Slope :

=  rise / run 

=  (-3 - 5)/(0 - 0)

=  -8/0

=  undefined

The slope is undefined. 

5. Answer :

Equation of vertical lines will be in the form of y = k

Here k may be positive or negative. 

Considering the given point (5, -3), the value of y is -3. Then the equation will be y = -3.

So, the required equation of the vertical line passes through the point (5, -3) is y = -3. Option a is correct.

6 . Answer :

Equation of vertical lines will be in the form of y = k

Here k may be positive or negative. 

Considering the given point (-4, 5), the value of y is 5. Then the equation will be y = 5.

So, the required equation of the vertical line passes through the point (-4, 5) is y = 5. 

7. Answer :

Equation of horizontal lines will be in the form of x = h

Here k may be positive or negative. 

Considering the given point (3, 2), the value of x is 3. Then the equation will be x = 3

So, the required equation of the horizontal line passes through the point (3, 2) is x = 3.

8. Answer : 

Given lines are, y = 2x - 4, x = -1 and y = 2

Graphing y = 2x - 4 :

By observing the equation given above, it is in the form of y = mx + b. This must be slanting line.

Slope = 2 and y-intercept is -4.

To draw the graph of it, we have to start with y-intercept -4 and move up 2 units and move up 1 unit.

Finding x intercept :

Put y = 0

0 = 2x - 4

2x = 4

x = 4/2

x = 2

Graphing x = -1 :

The line which is in the form of x = h, must be vertical line.

Graphing y = 2 :

The line which is in the form of y = k, must be horizontal line.

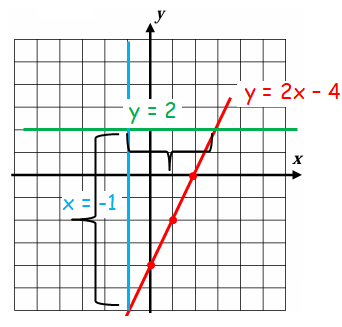
Finding area of triangle which is covered by these lines :

Base = 4, height = 8

Area of triangle = (1/2) x base x height

= (1/2) x 4 x 8

= 16 square units.

9 . Answer :

The line shown above is the vertical line, equation will be in the form y = k.

The line passes through the point -4, then the required equation will be y = -1.

10. Answer :

The line shown above is the horizontal line, equation will be in the form x = h.

The line passes through the point 4, then the required equation will be x = 4.

11. Answer :

Equation of slant line :

By observing the graph, y-intercept of the line is y = 1. To find slope, let us find two points lie on the line.

(1, -1) and (2, -3)

Slope (m) = (-3 + 1) / (2 - 1)

= -2/1

Slope (m) = -2

Equation of the line will be in the form y = mx + b

y = -2x + 1

Equation of horizontal line :

y = -5 

Equation of vertical line :

x = -2

From the above shaded region of triangular part,

Base = 5, height = 10

Area of the triangle = (1/2) x base x height

= (1/2) x 5 x 10

= 25 square units

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.