SLOPES OF HORIZONTAL AND VERTICAL LINES

The slope of a line is the ratio of rise to run for any two points on the line. 

slope  =  rise / run  =  change in y / change in x

Find the slope of each line.

Example 1 : 

Solution : 

Slope :

=  rise / run 

=  (2 - 2)/[3 - (-1)]

=  0/(3 + 1)

=  0/4

=  0

The slope is 0. 

Example 2 : 

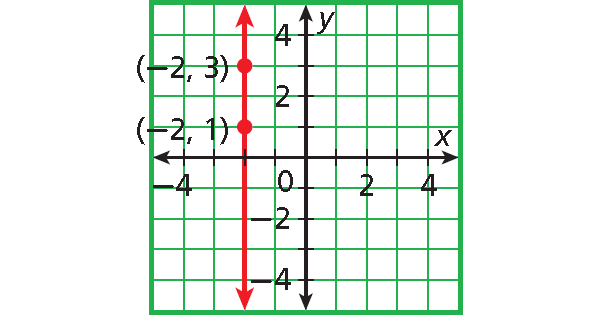
Solution : 

Slope :

=  rise / run 

=  (1 - 3)/[-2 - (-2)]

=  -2/(-2 + 2)

=  -2/0

=  undefined

The slope is undefined. 

Example 3 : 

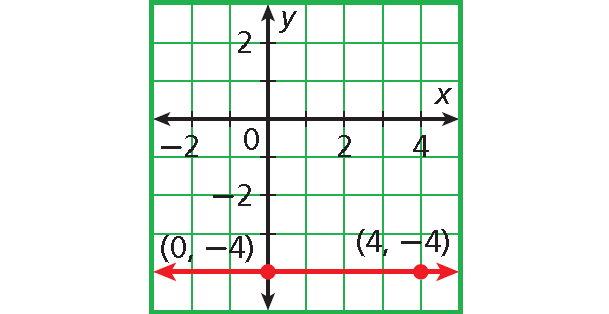
Solution : 

Slope :

=  rise / run 

=  [-4 - (-4))/(4 - 0)

=  (-4 + 4)/4

=  0/4

=  0

The slope is 0. 

Example 4 : 

Solution : 

Slope :

=  rise / run 

=  (-3 - 5)/(0 - 0)

=  -8/0

=  undefined

The slope is undefined. 

Zero Slope

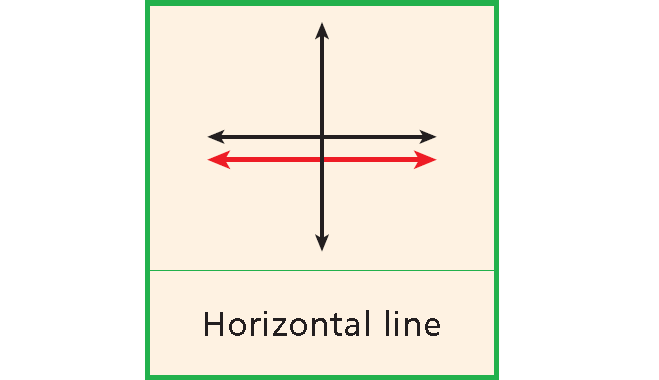
The slope of any horizontal line is zero. 

Undefined Slope

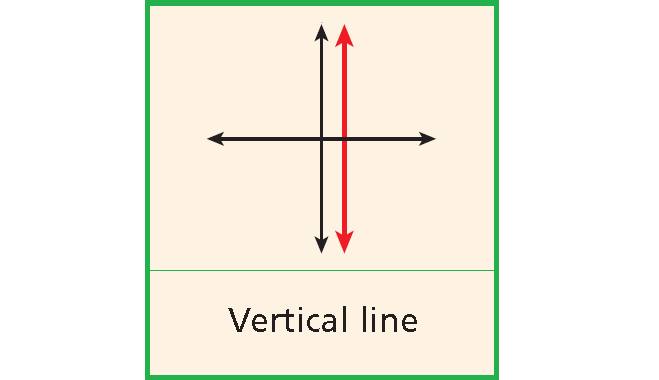
The slope of any vertical line is undefined. 

Example 5 :

Which of the following statements is true about the graph of the equation

2x - 3y = -4

in the xy-plane?

a) It has a negative slope and a positive y-intercept.

b) It has a negative slope and a negative y-intercept.

c) It has a positive slope and a positive y-intercept.

d) It has a positive slope and a negative y-intercept.

Solution :

To find slope and y-intercept from the equation which is in standard form, we have to convert into slope intercept form.

2x - 3y = -4

2x + 4 = 3y

y = (2/3)x + (4/3)

Comparing with y = mx + b

Slope (m) = 2/3 and y-intercept (b) = 4/3

From this, we know that both slope and y-intercepts are positive.

Example 6 :

The front of a roller coaster car is at the bottom of the hill and 15 feet above the ground. If the front of the roller coaster car rises at a constant rate of 8 feet per second, which of the following equations gives the height h in feet, of the front of the roller coaster car s seconds after it starts up the hill ?

a)  h = 8s + 15      b)  h = 15s + 335/8

c)  h = 8s + 335/15       d)  h = 15s + 8

Solution :

Initial height of the roller coaster = 15 feet

y-intercept = 15

It rises at the constant rate of 8 feet per second, then slope = 8

The required equation will be in the form, h = ms + b

Here h is the height and s is seconds taken and b is the y-intercept. Applying known values, we get

h = 8s + 15

Then option a is correct.

Example 7 :

C =75h + 125

The equation above gives the amount C, in dollars, an electrician charges for a job that takes h hours. Ms.Sanchez and  Mr.Roland each hired this electrician.

The electrician worked 2 hours longer on  Ms.Sanchez’s job than on Mr.Roland’s job. How much more did the electrician charge Ms.Sanchez than Mr.Roland?

A) $75    B) $125    C) $150     D) $275

Solution :

Let us consider, the electrician is working 5 hours in Ms.Sanchez home.

Amount paid by Ms.Sanchez :

C = 75h + 125

when h = 5

C = 75(5) + 125

C = 375 + 125

= 500

Amount paid by Mr.Roland :

Since he is working 2 more hours in Mr.Roland, to find the amount paid by Mr.Roland, we have to apply h = 7

C = 75(7) + 125

C = 525 + 125

= 650

Difference amount = 650 - 500

= 150

So, the required difference amount is $150.

Example 8 :

The line graphed in the xy plane below models the total cost in dollars, for a car ride, y in a certain city during non peak hours based on the number of miles travelled x.

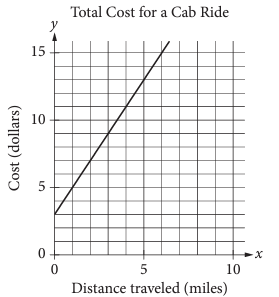
According to the graph, what is the cost of each additional miles travelled in dollars of a car ride ?

a)  $2     b)  $2.60    c)  $3     d) $5

Solution :

Choosing two points on the line, (0, 3) and (1, 5)

Using the formula to find slope,

m = (y₂ - y₁) / (x₂ - x₁)

= (5 - 3) / (1 - 0)

= 2/1

Slope = 2

So, the answer is option a.

Example 9 :

Line m in the xy plane contains the points (2, 4) and (0, 1). Which of the following is an equation of line m ?

a)  y = 2x + 3             b)  y = 2x + 4

c)  y = (3/2)x + 3          d) y = (3/2) x + 1

Solution :

(2, 4) and (0, 1)

Slope = (1 - 4) / (0 - 2)

= -3/(-2)

= 3/2

Equation of the line :

y = mx + b

y = (3/2)x + b

Applying the point (0, 1).

1 = (3/2)(0) + b

b = 1

Applying the value of b, we get 

y = (3/2)x + 1

So, option d is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.