SOLVE ABSOLUTE VALUE EQUATIONS
To solve any absolute value function, it has to be in the form of
|x + a| = k
Here, a and k are real numbers. And there should be only absolute part on the left side.
Let us consider the absolute value equation given below.
|2x + 3| = 5
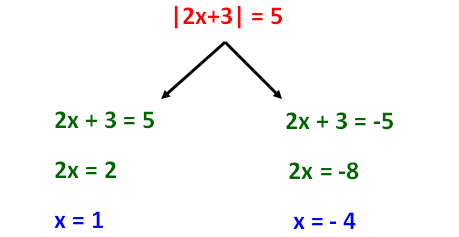
The following steps will be useful to solve absolute value equations.
Step 1 :
Get rid of absolute sign and divide it into two branches.
Step 2 :
For the first branch, take the sign as it is on the right side.
Step 3 :
For the second branch, change the sign on the right side.
Step 4 :
Then solve both the branches.
Example 1 :
Solve for m :
|6m| = 42
Solution :
|
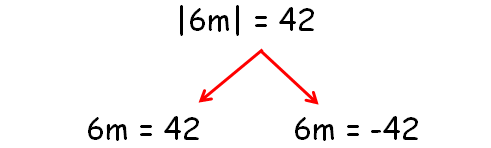
6m = 42 Divide each side by 6. m = 7 |
6m = 42 Divide each side by 6. m = -7 |
Example 2 :
Solve for x :
|6x| = 30
Solution :
|
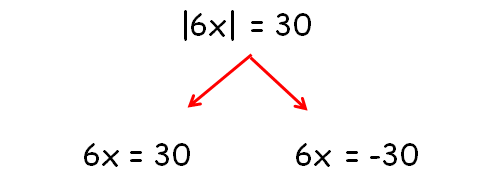
6x = 30 Divide each side by 6. x = 5 |
6x = -30 Divide each side by 6. x = -5 |
Example 3 :
Solve for k :
|k - 10| = 3
Solution :
|
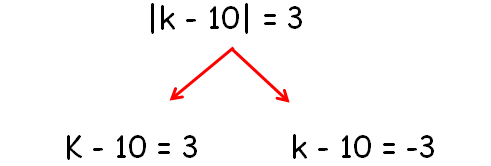
k - 10 = 3 Add 10 to each side. k = 13 |
k - 10 = -3 Add 10 to each side. k = 7 |
Example 4 :
Solve for x :
|x/7| = 3
Solution :
|
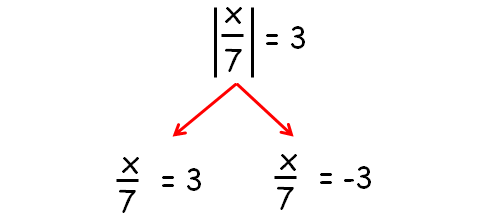
x/7 = 3 Multiply each side by 7. x = 21 |
x/7 = -3 Multiply each side by 7. x = -21 |
Example 5 :
Solve for a :
|a - 5|/8 = 5
Solution :
|a - 5|/8 = 5
Multiply each side by 8.
|a - 5| = 40
|
a - 5 = 40 Add 5 to each side. a = 45 |
a - 5 = -40 Add 5 to each side. a = -35 |
Example 6 :
Solve for p :
-3|p| = -12
Solution :
-3|p| = -12
Divide each side by -3.
|p| = 4
|
p = 4 |
p = -4 |
Example 7 :
Solve for m :
|7m| + 3 = 73
Solution :
|7m| + 3 = 73
Subtract 3 from each side.
|7m| = 70
|
7m = 70 Divide each side by 7. m = 10 |
7m = -70 Divide each side by 7. m = -10 |
Example 8 :
Solve for v :
-10|v + 2| = -70
Solution :
-10|v + 2| = -70
Divide each side by -10.
|v + 2| = 7
|
v + 2 = 7 Subtract 2 from each side. v = 5 |
v + 2 = -7 Subtract 2 from each side. v = -9 |
Example 9 :
Solve for v :
|-9 + v|/8 = 3
Solution :
|-9 + v|/8 = 3
Multiply each side by 8.
|-9 + v| = 24
|
-9 + v = 24 Add 9 to each side. v = 33 |
-9 + v = -24 Add 9 to each side. v = -15 |
Example 10 :
Solve for n :
|n| + 1 = 2
Solution :
|n| + 1 = 2
Subtract 1 on both sides.
|n| = 1
|
n = 1 |
n = -1 |
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
De Moivre's Theorem and Its Applications
Apr 19, 24 08:30 AM
De Moivre's Theorem and Its Applications -
First Fundamental Theorem of Calculus - Part 1
Apr 17, 24 11:27 PM
First Fundamental Theorem of Calculus - Part 1 -
Polar Form of a Complex Number
Apr 16, 24 09:28 AM
Polar Form of a Complex Number
