SOLVE EQUATIONS IN COMPLEX NUMBERS WITH CUBE ROOTS OF UNITY
Question 1 :
Solve the equation z3 + 27 = 0.
Solution :
z3 + 27 = 0
z3 = -27
z3 = (-1 ⋅ 3)3
z = [(-1 ⋅ (3)3] 1/3
= 3 (-1)1/3
Polar form of -1 :
-1 = 3[cos π + i sin π]
= [cos(2kπ + π) + i sin (2kπ + π)]
= [cos π(2k + 1)) + i sin π(2k + 1)]
(-1)1/3 = [cos π(2k + 1)) + i sin π(2k + 1)]1/3
(-1)1/3 = [cos (π/3)(2k + 1)) + i sin (π/3)(2k + 1)]
k = 0, 1, 2
If k = 0
= [cos (π/3)(2k + 1)) + i sin (π/3)(2k + 1)]
= 3 cis (π/3)
If k = 1
= 3 [cos π + i sin π]
= -3
If k = 2
= [cos (5π/3) + i sin (5π/3)]
= 3 cis (5π/3)
Question 2 :
If ω ≠ 1 is a cube root of unity, show that the roots of the equation (z −1)3 + 8 = 0 are −1, 1− 2ω, 1− 2ω2
Solution :
(z −1)3 + 8 = 0
(z −1)3 = -8
(z −1) = (-8)1/3
(z −1) = -2 ⋅ (1) 1/3
z = -2 ⋅ (1) 1/3 + 1
z = 1 - 2 ⋅ (1) 1/3
Cube root of 1 are 1, ω, ω2
z = 1 - 2 ⋅ 1
z = 1 - 2 = -1
z = 1 - 2 ⋅ ω
z = 1 - 2ω
z = 1 - 2 ⋅ ω2
z = 1 - 2ω2
Question 3 :
Find the value of
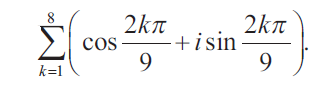
Solution :
If k = 1,
= cos 2π/9 + i sin 2π/9 ----(1)
If k = 2,
= cos 4π/9 + i sin 4π/9 ----(2)
If k = 3,
= cos 6π/9 + i sin 6π/9 ----(3)
If k = 4,
= cos 8π/9 + i sin 8π/9 ----(4)
...................
By adding all these, we get
= cis (π/9) (2 + 4 + 6 + 8 + 10 + 12 + 14 + 16)
= cis (π/9) 2(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8)
= cis (72π/9)
= cis 8π
= cos 8π + i sin 8π
= 1 + i(0)
= 1
Question 4 :
If ω ≠ 1 is a cube root of unity, show that
(i) (1 − ω + ω2)6 + (1 + ω − ω2)6 = 128.
(ii) (1 − ω)(1 + ω2)(1 + ω4)(1 + ω8).............(1 + ω2^11) = 1
Solution :
(i) (1 − ω + ω2)6 + (1 + ω − ω2)6 = 128.
L.H.S:
= (1 + ω2 − ω)6 + (1 + ω − ω2)6
= (- ω − ω)6 + (-ω2 − ω2)6
= (- 2ω) 6 + (- 2ω2) 6
= 64 ω6 + 64ω12
= 64 (ω3)2 + 64 (ω3)4
= 64 + 64
= 128
R.H.S
Hence proved.
(ii) (1 − ω)(1 + ω2)(1 + ω4)(1 + ω8).............(1 + ω2^11) = 1
L.H.S
(1 − ω)(1 + ω2)(1 + ω4)(1 + ω8)(1 + ω16) (1 + ω32) (1 + ω64)
(1 + ω128)(1 + ω256)(1 + ω512)(1 + ω1024)(1 + ω2048)
First 2 terms are = (1 − ω)(1 + ω2)
3rd and 4th terms :
(1 + ω4)(1 + ω8) = (1 + ω)(1 + ω2)
5th and 6th terms :
(1 + ω16)(1 + ω32) = (1 + ω)(1 + ω2)
Similarly by grouping these terms, we get
= [(1 + ω)(1 + ω2)]6
= [1 + ω2 + ω + ω3 ]6
= [0 + ω3 ]6
= 1
Hence proved.
Question 5 :
If z = 2 - 2i, find rotation of z by θ radians in the counter clock wise direction about the origin when
(i) θ = π/3 (ii) θ = 2π/3 (iii) θ = 3π/2
Solution :
z = 2 - 2i
Finding modulus :
z = √22 + (-2)2
z = √4 + 4
z = 2√2
Finding argument :
α = tan-1|(-2)/2|
α = tan-1|(-2)/2|
α = tan-1|-1|
α = π/4
Since (2, -2) lies in the fourth quadrant, θ = -α
Then θ = -π/4
2 - 2i = 2√2 (cos (-π/4) + i sin (-π/4))
i)
z is rotated by π/3 in counter clock wise direction, then
2 - 2i = 2√2 (cos (π/3 - π/4) + i sin (π/3 - π/4))
= 2√2 (cos (4π - 3π)/12) + i sin (4π - 3π)/12)
= 2√2 (cos (π/12) + i sin (π/12))
ii)
z is rotated by 2π/3 in counter clock wise direction, then
2 - 2i = 2√2 (cos (2π/3 - π/4) + i sin (2π/3 - π/4))
= 2√2 (cos (8π - 3π)/12) + i sin (8π - 3π)/12)
= 2√2 (cos (5π/12) + i sin (5π/12))
iii)
z is rotated by 3π/2 in counter clock wise direction, then
2 - 2i = 2√2 (cos (3π/2 - π/4) + i sin (3π/2 - π/4))
= 2√2 (cos (6π - π)/4) + i sin (6π - π)/4)
= 2√2 (cos (5π/4) + i sin (5π/4))
Question 6 :
If
[(1 + i)/(1 - i)]3 - [(1 - i)/(1 + i)]3 = x + iy
then find (x, y).
Solution :
[(1 + i)/(1 - i)]
To convert it as complex number, we have to multiply both numerator and denominator by the conjugate of the denominator.
= [(1 + i)/(1 - i)] [(1 + i) / (1 + i)]
= (1 + i)(1 + i)/(1 - i)(1 + i)
= (12 + i + i + i2) / (12 - i2)
= (12 + 2i - 1) / (1+1)
= 2i/2
[(1 + i)/(1 - i)] [(1 + i) / (1 + i)] = i