SOLVE PROPORTIONS

When two ratios expressed in its simplest form are equal they are said to be in proportion.

Proportion is represented by the symbol ‘ = ‘ or ‘::‘

If the ratio a: b is equal to the ratio c : d then a,b,c,d are said to be in proportion.

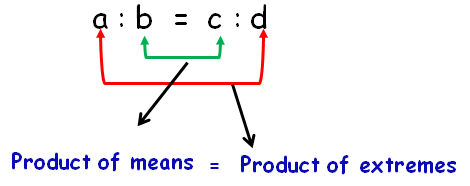
If a : b and c : d are in proportion then a x d = b x c.

The proportion is written as a : b :: c : d.

In a proportion, the product of extremes is equal to the product of means.

Example 1 :

Find the missing term in 3 : 4 = 12 : __.

Solution :

Let x be the missing term.

3 : 4 = 12 : x

Since the ratios 3 : 4 is equal to 12 : x, 3, 4, 12 and x are said to be in proportion.

That is,

Product of extremes = Product of means

3x = 4(12)

Divide each side by 3.

x = 16

So, the missing term is 16.

Example 2 :

Using 3 and 12 as means, write any two proportions.

Solution :

Given 3 and 12 are means.

Then,

__ : 3 = 12 : __

Let 'a' and 'b' be the missing terms.

The product of the means 3 x 12 = 36.

The product of Extremes (a x b) must be 36.

36 can be written as 2 x 18 or 4 x 9 etc,

2 : 3 = 12 : 18

4 : 3 = 12 : 9

Example 3 :

Using 4 and 20 as means, write two proportions.

Solution :

Given 3 and 12 are means.

Then,

__ : 4 = 20 : __

Let 'a' and 'b' be the missing terms.

The product of the means 4 x 20 = 80.

The product of Extremes (a x b) must be 80.

80 can be written as 16 x 5 or 10 x 8 etc,

16 : 4 = 20 : 5

10 : 4 = 20 : 8

Example 4 :

Show that 12 : 9, 4 : 3 are in proportion.

Solution :

The product of the extremes = 12 x 3 = 36.

The product of the means = 9 x 4 = 36.

12 : 9, 4 : 3 are in proportion

(i.e.) 12 : 9 :: 4 : 3

Example 5 :

Solve for x :

5/3 = x/48

Solution :

5/3 = x/48

5(48) = x(3)

Divide each side by 3.

80 = x

Example 6 :

Solve for a :

18/a = 9/50

Solution :

18/a = 9/50

18(50) = a(9)

Divide each side by 9.

100 = a

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.