SOLVED PROBABILITY PROBLEMS

Problem 1 :

Two dice are rolled, find the probability that the sum is

i) equal to 1 ii) equal to 4 iii) less than 13

Solution :

Sample space : 

{(1, 1)(1, 2)(1, 3)(1, 4)(1, 5)(1, 6)(2, 1)(2, 2)(2, 3)(2, 4)(2, 5)(2, 6)(3, 1)(3, 2)(3, 3)(3, 4)(3, 5)(3, 6)(4, 1)(4, 2)(4, 3)(4, 4)(4, 5)(4, 6)(5, 1)(5, 2)(5, 3)(5, 4)(5, 5)(5, 6)(6, 1)(6, 2)(6, 3)(6, 4)(6, 5)(6, 6)}

n(S)  =  36

Let "A" be the event of getting sum equal to 1.

A = 0

n(A)  =  0

p(A)  =  n(A)/n(S)  =  0/36

p(A)  =  0

(ii) equal to 4 

Let "B" be the event of getting the sum equal to 4.

B = {(1, 3) (2, 2) (3, 1)}

n(B)  =  3

p(B)  =  n(B)/n(S)  

P(B)  =  3/36

P(B)  =  1/12

(iii) less than 13

C = {(1, 1)(1, 2)(1, 3)(1, 4)(1, 5)(1, 6)(2, 1)(2, 2)(2, 3)(2, 4)(2, 5)(2, 6)(3, 1)(3, 2)(3, 3)(3, 4)(3, 5)(3, 6)(4, 1)(4, 2)(4, 3)(4, 4)(4, 5)(4, 6)(5, 1)(5, 2)(5, 3)(5, 4)(5, 5)(5, 6)(6, 1)(6, 2)(6, 3)(6, 4)(6, 5)(6, 6)}

n(C)  =  36

p(C)  =  n(C)/n(S)

  =  36/36

p(C)  =  1

Problem 2 :

A manufacturer tested 7000 LED lights at random and found that 25 of them were defective. If a LED light is selected at random, what is the probability that the selected LED light is a defective one.

Solution :

Total number of bulbs n(S)  =  7000

Number of defective bulbs  =  25

Let ""A be the event of getting defective bulb

n(A)  =  25

p(A)  =  n(A)/n(S)

p(A)  =  25/7000

p(A)  =  1/280

Problem 3 :

In a football match, a goalkeeper of a team can stop the goal, 32 times out of 40 attempts tried by a team. Find the probability that the opponent team can convert the attempt into a goal.

Solution :

Total number of match n(S)  =  40

Let "A" be the event of the opponent team can convert attempt into goal

n(A)  =  40 - 32  =  8

p(A)  =  n(A)/n(S)  

P(A)  =  8/40

P(A)  =  1/5

Problem 4 :

What is the probability that the spinner will not land on a multiple of 3?

Solution :

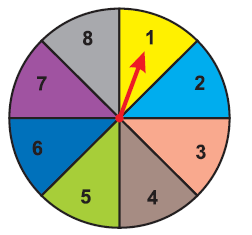
Sample space  =  {1, 2, 3, 4, 5, 6 , 8}

n(S)  =  8

Let "A" be the event of that the spinner will not land in multiple of 3.

A = {1, 2, 4, 5, 7, 8}

n(A)  =  6

P(A)  =  n(A) / n(S)

P(A)  =  6/8

P(A)  =  3/4

Problem 5 :

Frame two problems in calculating probability, based on the spinner shown here.

Solution :

(i)  What is the probability that the spinner will land on a multiple of 2 ?

(ii)  What is the probability that the spinner will land on a number greater than 3 ?

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.