SOLVED PROBLEMS ON DETERMINANTS

Problem 1 :

Without expanding the determinant, prove that

Solution

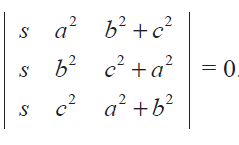
Problem 2 :

Show that 

Solution

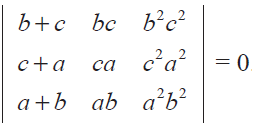
Problem 3 :

Prove that

Solution

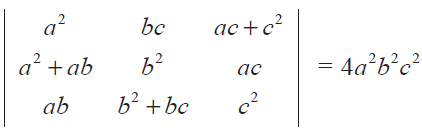
Problem 4 :

Prove that

Solution

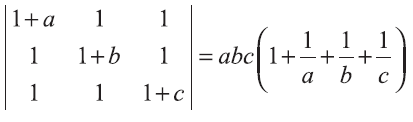
Problem 5 :

Prove that

Solution

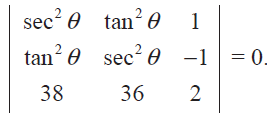
Problem 6 :

Show that 

Solution

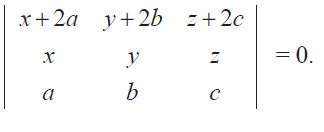
Problem 7 :

Write the general form of a 3 × 3 skew-symmetric matrix and prove that its determinant is 0.    Solution

Problem 8 :

If

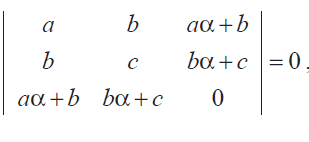
prove that a, b, c are in G.P. or a is a root of ax² + 2bx + c = 0.             Solution

Problem 9 :

prove that

Solution

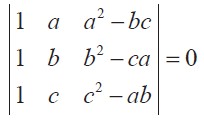
Problem 10 :

If a, b, c are p^th, q^th and r^th terms of an A.P, find the value of

Solution

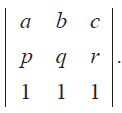
Problem 11:

Prove that

Solution

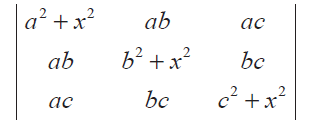
Problem 12 :

If a, b, c are all positive, and are p^th, q^th and r^th terms of a G.P., show that

Solution

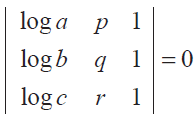
Problem 13 :

Find the value of 

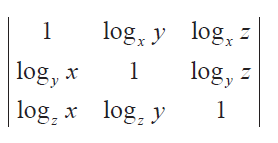
if x, y and z ≠ 1       Solution

Problem 14 :

If A =

Solution

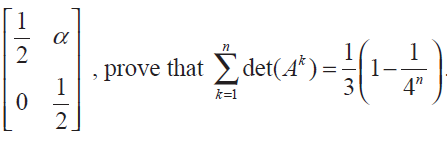
Problem 15 :

Without expanding, evaluate the following determinants

Solution

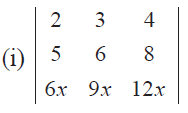
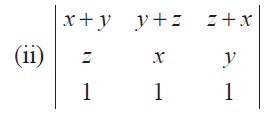
Problem 16 :

If A is a square matrix and | A | = 2, find the value of |AA^T| .                 Solution

Problem 17 :

If A and B are square matrices of order 3 such that | A | = -1 and |B| = 3, find the value of |3AB|.      Solution

Problem 18 :

If λ = - 2, determine the value of

Solution

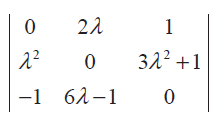
Problem 19 :

Determine the roots of the equation

Solution

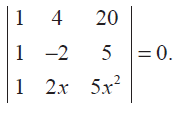
Problem 20 :

Verify that det(AB) = (det A) (det B) for

Solution

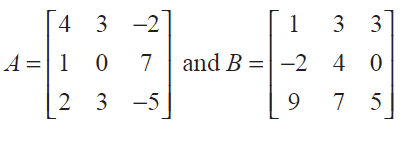
Problem 21 :

Using cofactors of elements of second row, evaluate | A |, where

Solution

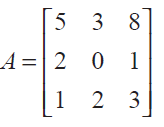
Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.