SOLVING ABSOLUTE VALUE EQUATIONS

The general form of an absolute value equation is

|ax + b| = k

In the above absolute value equation, we can notice that there is only absolute part on the left side. 

(Here 'a' and 'k' are real numbers and k ≥ 0)

Let us consider the absolute value equation |2x + 3| = 5.

We can solve the absolute value equation |2x + 3| = 5 as shown below. 

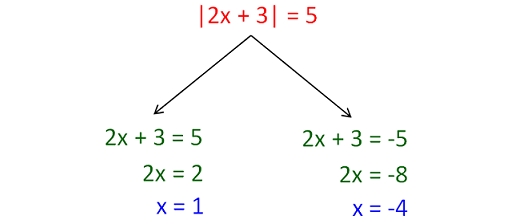
The following steps will be useful to solve absolute value equations.

Step 1 :

Get rid of absolute sign and divide it into two branches. 

Step 2 :

For the first branch, take the sign as it is on the right side.  

Step 3 :

For the second branch, change the sign on the right side.

Step 4 :

Then solve both the branches. 

Solve the following absolute value equations :

Example 1 :

Solve the absolute value equation :

|3x + 5|  =  7

Solution :

|3x + 5| = 7

3x + 5 = 7  or  3x + 5 = -7

3x = 2  or  3x = -12

x = 2/3  or  x = -4

Example 2 :

Solve the absolute value equation :

|7x|  =  21

Solution :

|7x| = 21

7x = 21  or  7x = -21

x = 3  or  x = -3

Example 3 :

Solve the absolute value equation :

|2x + 5| + 6  =  7

Solution :

|2x + 5| + 6 = 7

Subtract 6 from each side.

|2x + 5| = 1

2x + 5 = 1  or  2x + 5 = 1

2x = -4  or  2x = -6

x = -2  or  x = -3

Example 4 :

Solve the absolute value equation : 

|x - 3| + 6  =  6

Solution :

|x - 3| + 6 = 6

Subtract 6 from each side.

|x - 3| = 0

x - 3 = 0

x = 3

Example 5 :

Solve the absolute value equation :

2|3x +4|  =  7

Solution :

2|3x +4| = 7

Divide each side by 2. 

|3x + 4| = 7/2

3x + 4 = 7/2  or  3x + 4 = -7/2

3x = 7/2 - 4  or  3x = -7/2 - 4

3x = -1/2  or  3x = -15/2

x = -1/6  or  x = -15/6

x = -1/6  or  x = -5/2

Example 6 :

Solve the absolute value equation :

3|5x - 6| - 4  =  5

Solution :

3|5x - 6| - 4 = 5

Add 4 to each side.

3|5x - 6| = 9

Divide each side by 3.

|5x - 6| = 3

5x - 6 = 3  or  5x - 6 = -3

5x = 9  or  5x = 3

x = 9/5  or  x = 3/5

Example 7 :

Solve the absolute value equation :

|x² - 4x - 5| = 7

Solution :

|x² - 4x - 5| = 7

x² - 4x  - 5 = 7  or  x² - 4x - 5 = -7

x² - 4x  - 12 = 0  or  x² - 4x + 2 = 0

Solve the first quadratic equation x² - 4x - 12 = 0.

x² - 4x  - 12 = 0

(x + 2)(x - 6) = 0

x + 2 = 0  or  x - 6 = 0

x = -2  or  x = 6

Solve the second quadratic equation x² - 4x + 2 = 0.

This quadratic equation can not be solved by factoring. So, we can use quadratic formula and solve the equation as shown below.

Comparing ax² + bx + c = 0 and x² - 4x + 2 = 0, we get

a = 1, b = -4, c = 2

Quadratic formula :

Substitute a = 1, b = -4 and c = 2.

So, the solution is x  =  -2, 7, 2 ± √2.

Example 8 :

Solve the absolute value equation :

0.5|0.5x| - 0.5  =  2.5

Solution :

0.5|0.5x| - 0.5 = 2.5

Add 0.5 to each side. 

0.5|0.5x| = 3

Divide each side by 0.5

|0.5x| = 6

0.5x = 6  or  0.5x = -6

x = 12  or  x = -12

Example 9 :

If the absolute value equation |2x + k|  =  3 has the solution x  =  -2, find the value of k. 

Solution :

Because x = -2 is a solution, substitute x = -2 in the given absolute value equation. 

|2(-2) + k| = 3

|-4 + k| = 3

Solve for k :

-4 + k = 3  or  -4 + k = -3

k = 7  or  k = 1

Example 10 :

If the absolute value equation |x - 3| - k = 0 has the solution x  =  -5, find the value of k. 

Solution :

Because x = -2 is a solution, substitute x = -2 in the given absolute value equation. 

|-5 - 3| - k = 0

|-8| - k = 0

8 - k = 0

8 = k

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.