SOLVING COMPOUND INEQUALITIES WORKSHEET

Problem 1 :

Solve the compound inequality. Then graph the solution set

k + 2 > 12 and k + 2 ≤ 18

Problem 2 :

Solve the following inequality and graph the solution

3 < 2x - 3 < 15

Problem 3 :

Solve the following inequality and graph the solution

3t – 7 ≥ 5 and 2t + 6 ≤  12

Problem 4 :

Solve the following inequality and graph the solution

4m - 5 > 7 or 4m - 5 < -9

Detailed Answer Key

Problem 1 :

Solve the compound inequality. Then graph the solution set

k + 2 > 12 and k + 2 ≤ 18

Solution :

By graphing the inequality k > 10, we get the graph given below.

By graphing the inequality ≤ 16, we get the graph given below.

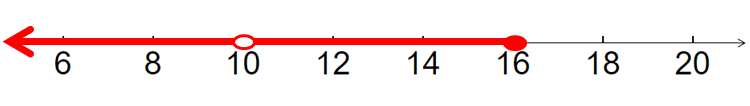
By combining the above two graphs, we get the common region between 10 and 16.

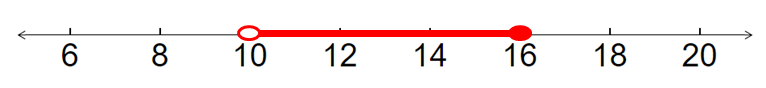
Problem 2 :

Solve the following inequality and graph the solution

3 < 2x - 3 < 15

Solution :

3 < 2x - 3 < 15

Add 3 on both sides

3 + 3 < 2x – 3 + 3 < 15 + 3

6 < 2x < 18

Divide by 2

6/2 < 2x/2 < 18/2

3 < x < 9

Problem 3 :

Solve the following inequality and graph the solution

3t – 7 ≥ 5 and 2t + 6 ≤  12

Solution :

3t – 7 ≥ 5 and 2t + 6 ≤  12

t  ≥ 4 and t ≤  3

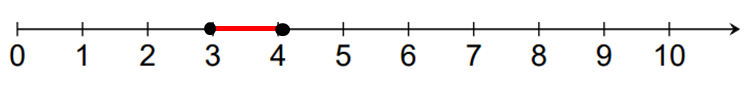
Problem 4 :

Solve the following inequality and graph the solution

4m - 5 > 7 or 4m - 5 < -9

Solution :

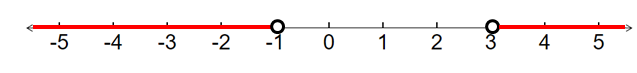
Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.