SOLVING EQUATIONS FOR TRIVIAL AND NON TRIVIAL SOLUTIONS

Question 1 :

Solve the following system of homogenous equations.

(i) 3x + 2y + 7z = 0, 4x − 3y − 2z = 0, 5x + 9y + 23z = 0

Solution :

rank of (A) is 2 and rank of (A, B) is 2 < 3.

3x + 2y + 7z  =  0 -----(1)

-17y - 34z  =  0 -----(2)

Let z = t

-17y  =  34t

y  =  34t/(-17)  =  -2t

By applying the value of z in (1), we get

3x + 2(-2t) + 7t  =  0

3x - 4t + 7t  =  0

3x  =  -3t

x  =  -t

Hence the solution is (-t, -2t, t)

(ii) 2x + 3y − z = 0, x − y − 2z = 0, 3x + y + 3z = 0

Solution :

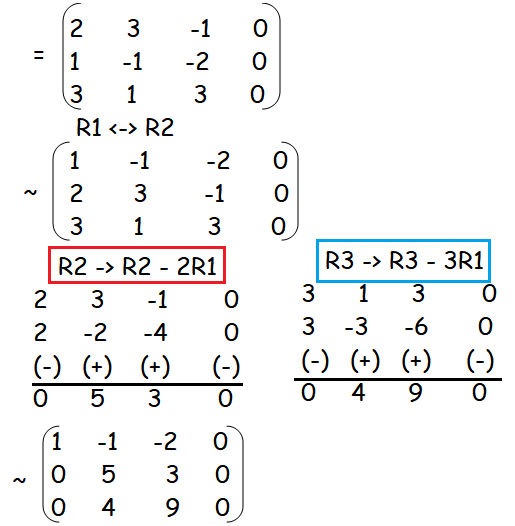
Rank of A is 3 and rank of (A, B) is 3.

Since rank of A and rank of (A, B) are equal, it has trivial solution.

Question 2 :

Determine the values of λ for which the following system of equations x + y + 3z = 0, 4x + 3y + λz = 0, 2x + y + 2z = 0 has (i) a unique solution (ii) a non-trivial solution.

Solution :

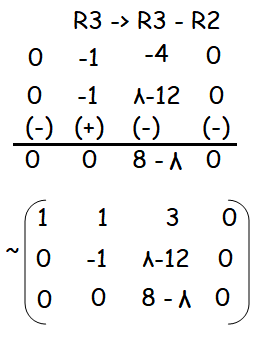
(i) a unique solution

If λ ≠ 8, then rank of A and rank of (A, B) will be equal to 3.It will have unique solution.

(ii) a non-trivial solution.

If λ = 8, then rank of A and rank of (A, B) will be equal to 2.It will have non trivial solution.

Question 3 :

By using Gaussian elimination method, balance the chemical reaction equation :

C₂ H₆ + O₂ -> H₂O + CO₂

Solution :

x₁ C₂ H₆ + x₂ O₂ -> x₃ H₂O + x₄ CO₂  ----(1)

The number of carbon atoms on the left-hand side of (1) should be equal to the number of carbon atoms on the right-hand side of (1). So we get a linear homogenous equation

2x₁   =  x₄  (carbon)

2x₁ - x₄  =  0  ----(1)

6x₁   =  2x₃  (Hydrogen)

6x₁ - 2x₃  =  0  ----(2)

2x₂  =  1x₃ + 2x₄ (Oxygen)

2x₂ - x₃ - 2x₄  =  0  ----(3)

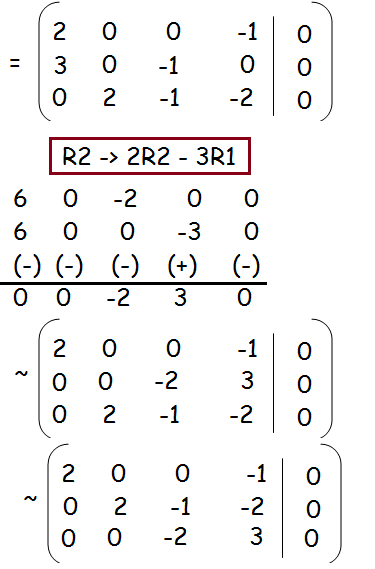
rank of A is 3 = rank of (A, B) = 3 < 4

Then the system is consistent and it has infinitely many solution.

2x₁ + 0x₂ + 0x₃ - x₄  =  0   ---(A)  

2x₂ - x₃ - 2x₄  =  0   ---(B)

-2x₃ + 3x₄  =  0   ---(C)

Let x₄  =  t

-2x₃  = -3t

x₃  = 3t/2

By applying the value of x₃ in (B), we get

2x₂ - (3t/2) - 2t  =  0

2x₂ =  (3t/2) + 2t

2x₂ =  (7t/2)

x₂ =  (7t/4)

By applying the value of x₄ in (A), we get

2x₁ - t  =  0   

x₁  =  t/2

Let t = 4

x₁  =  2, x₂ =  7, x₃  = 6, x₄  =  4.

x₁ C₂ H₆ + x₂ O₂ -> x₃ H₂O + x₄ CO₂ 

2 C₂ H₆ + 7 O₂ -> 6 H₂O + 4 CO₂ 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.