SOLVING EQUATIONS WITH ABSOLUTE VALUES ON BOTH SIDES
The picture shown below explains how to solve the equations in which we have absolute value sign on both sides.
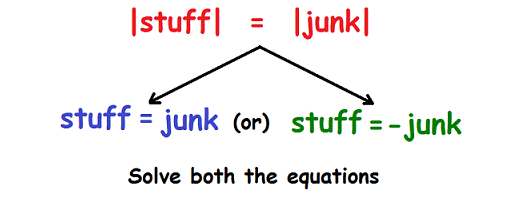
Example 1 :
Solve for x :
|x - 3| = |3x + 2|
Solution :
Based on the idea given above, we have
x - 3 = (3x + 2)
x - 3 = 3x + 2
- 5 = 2x
- 5/2 = x
(or)
x - 3 = -(3x + 2)
x - 3 = - 3x - 2
- 1 = - 4x
1/4 = x
Justify and evaluation :
Substitute x = -5/2 and x = 1/4 in the given absolute value equation.
|-5/2 - 3| = |3(-5/2) + 2|
|-11/2| = |-15/2 + 2|
|-11/2| = |-11/2|
11/2 = 11/2
|1/4 - 3| = |3(1/4) + 2|
|-11/4| = |3/4 + 2|
|11/4| = |11/4|
11/4 = 11/4
Substituting x = -5/2 and x = 1/4 into the original equation results in true statements.
Both the answers x = -5/2 and x = 1/4 are correct and acceptable.
Problem 2 :
Solve for x :
|x - 7| = |2x - 2|
Solution :
Based on the idea given above, we have
x - 7 = 2x - 2
x - 7 = 2x - 2
- 5 = x
(or)
x - 7 = - (2x - 2)
x - 7 = -2x + 2
3x = 9
x = 3
Justify and evaluation :
Substitute x = -5 and x = 3 in the given absolute value equation.
x = -5
|-5 - 7| = |2(-5) - 2|
|-12| = |-10 - 2|
|-12| = |-12|
12 = 12
x = 3
|3 - 7| = |2(3) - 2|
|-4| = |6 - 2|
|-4| = |4|
4 = 4
Substituting x = -5 and x = 3 into the original equation results in true statements.
Both the answers x = -5 and x = 3 are correct and acceptable.
Problem 3 :
Solve for z :
|2z + 5| = |2z - 1|
Solution :
Based on the idea given above, we have
2z + 5 = 2z - 1
5 = -1
5 = -1
The above statement is false.
No solution here.
(or)
2z + 5 = - (2z - 1)
2z + 5 = -2z + 1
4 = -4z
-1 = z
Justify and evaluation :
Substitute z = -1 in the given absolute value equation.
|2(-1) + 5| = |2(-1) - 1|
|-2 + 5| = |-2 - 1|
|3| = |-3|
3 = 3
Substituting z = -1 into the original equation results in true statement.
So, the answer z = -1 is correct and acceptable.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Pascal Triangle and Binomial Expansion
Feb 01, 25 10:12 AM
Pascal Triangle and Binomial Expansion - Concept - Examples -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Feb 01, 25 06:26 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 106)
Feb 01, 25 06:23 AM
Digital SAT Math Problems and Solutions (Part - 106)

