SOLVING EXPONENTIAL EQUATIONS WITH LOGARITHMS

Converting Equation From Exponential to Logarithm

Consider the following equation in exponential form.

b^y = a

The picture below illustrates how to convert the above equation from exponential to logarithmic form.

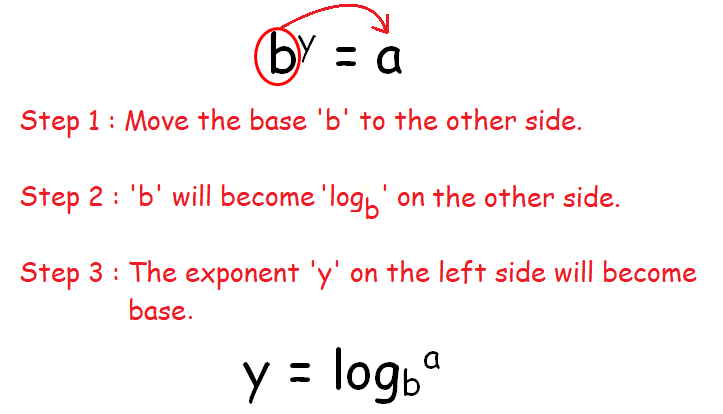
Still don't understand what is explained above, please watch the video below for step by step live explanation.

Example 1 :

Solve for x :

3^x = 27

Solution :

In the given equation, 27 is a power 3 (27 = 3³).

Method 1 :

3^x = 27

Convert the above equation to logarithm.

x = log₃27

x = log₃(3³)

Using the power rule of logarithm,

x = 3log₃3

x = 3(1)

x = 3

Method 2 :

3^x = 27

Take logarithm with the base 3 on both sides.

log₃3^x = log₃27

log₃(3^x) = log₃(3³)

xlog₃3 = 3log₃3

x(1) = 3(1)

x = 3

Example 2 :

Solve for x :

2^{x - 5} = 1/16

Solution :

In the given equation, 16 is a power 2 (16 = 2^-4).

Method 1 :

2^{x - 5} = 1/16

Convert the above equation to logarithm.

x - 5 = log₂(1/16)

x - 5 = log₂(1/2⁴)

x - 5 = log₂(2^-4)

Using the power rule of logarithm,

x - 5 = -4log₂2

x - 5 = -4(1)

x - 5 = -4

Add 5 to both sides.

x = 1

Method 2 :

2^{x - 5} = 1/16

Take logarithm with the base 2 on both sides.

log₂(2^{x - 5}) = log₂(1/16)

log₂(2^{x - 5}) = log₂(1/2⁴)

log₂(2^{x - 5}) = log₂(2^-4)

Using the power rule of logarithm,

(x - 5)log₂2 = -4log₂2

(x - 5)(1) = -4(1)

x - 5 = -4

Add 5 to both sides.

x = 1

Example 3 :

Solve for x :

2^x - 1 = 5

Solution :

2^x - 1 = 5

Add 1 to both sides.

2^x = 5

In the equation above, 5 is not a power of 2. So, take logarithm with any base on both sides and solve for x.

log(2^x) = log6

Using power rule of logarithm,

xlog2 = log6

Divide both sides by log2.

Example 4 :

Solve for x :

5^{x - 1} - 2^x = 0

Solution :

5^{x - 1} - 2^x = 0

Add 2^x to both sides.

5^{x - 1} = 2^x

In the equation above, 5 is not a power of 2 and also 2 is not a power of 5.

So, take logarithm with any base on both sides and solve for x.

log(5^{x - 1}) = log(2^x)

Using power rule of logarithm,

(x - 1)log5 = xlog2

Using distributive property,

xlog5 - log5 = xlog2

Subtract xlog2 from both sides.

xlog5 - log5 - xlog2 = 0

Add log5 to both sides.

xlog5 - xlog2 = log5

Factor.

x(log5 - log)2 = log5

Divide both sides by (log5 - log2).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.