SOLVING SYSTEMS OF EQUATIONS USING INVERSE MATRICES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
This method can be applied only when the coefficient matrix is a square matrix and non-singular. Consider the matrix equation AX = B ,
Pre-multiplying both sides of (1) by A−1, we get
A−1(AX) = A−1B
(A−1A) X = A−1B
IX = A−1B
X = A−1B
Solved Questions
Question 1 :
Solve the following system of linear equations by matrix inversion method:
(i) 2x + 5y = −2, x + 2y = −3
Solution :
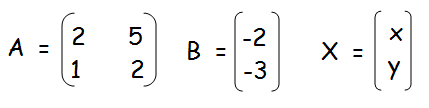
X = A-1 B
A-1 = (1/|A|) adj A
|A| = 4 - 5 = -1
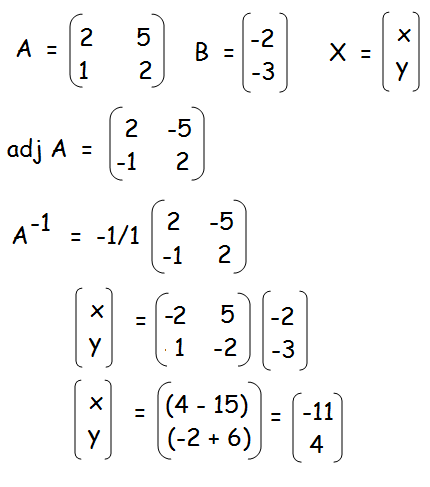
Hence the value of x and y are -11 and 4 respectively.
Question 2 :
(ii) 2x − y = 8, 3x + 2y = −2
Solution :
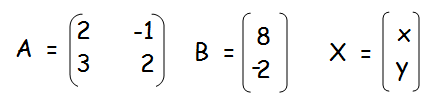
X = A-1 B
A-1 = (1/|A|) adj A
|A| = 4 + 3 = 7
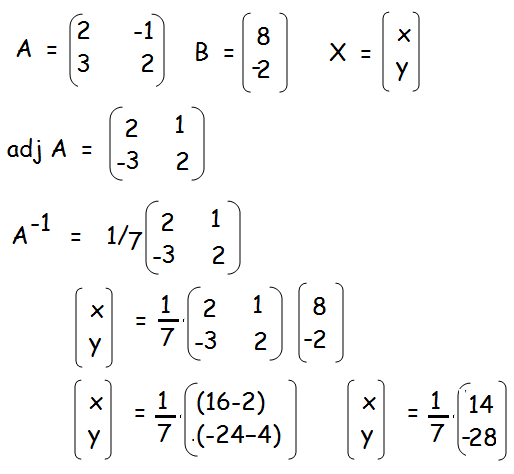
x = 14/7 = 2
y = -28/7 = -4
Hence the values of x and y are 2 and -4 respectively.
Question 3 :
(iii) 2x + 3y − z = 9, x + y + z = 9, 3x − y − z = −1
Solution :
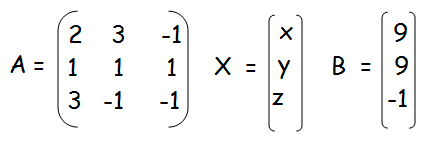
|A| = 2(-1 + 1) - 3(-1 - 3) - 1(-1 -3)
= 2(0) - 3(-4) - 1(-4)
= 12 + 4
|A| = 16
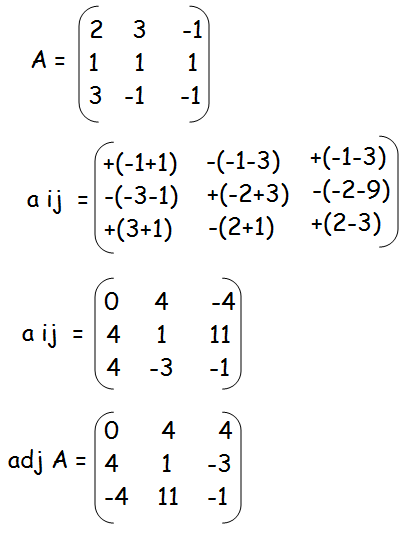
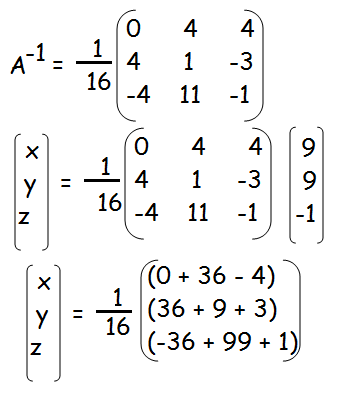
x = 32/16 = 2
y = 48/16 = 3
z = 64/16 = 4
Hence the values of x, y and z are 2, 3 and 4 respectively.
Question 4 :
(iv) x + y + z − 2 = 0, 6x − 4y + 5z − 31 = 0, 5x + 2y + 2z =13
Solution :
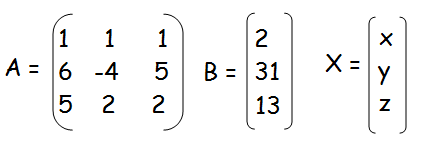
|A| = 1(-8 - 10) - 1(12 - 25) + 1(12 + 20)
= 1(-18) - 1(-13) + 1(32)
= -18 + 13 + 32
= 27
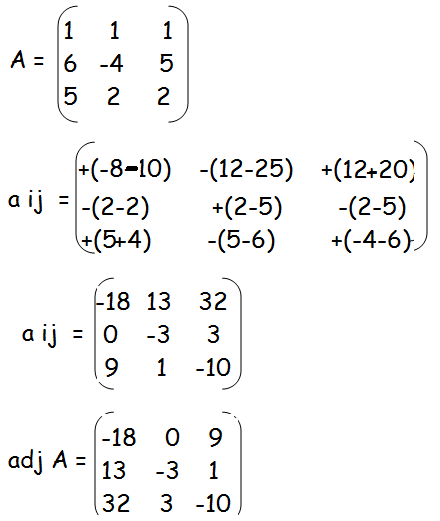
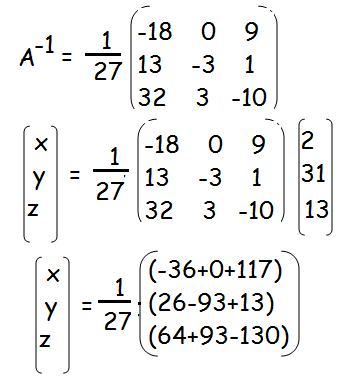
x = 81/27 = 3
y = -54/27 = -2
z = 27/27 = 1
Hence the values of x, y and z are 3, -2 and 1 respectively.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 40)
Dec 25, 25 08:30 AM
10 Hard SAT Math Questions (Part - 40) -
10 Hard SAT Math Questions (Part - 41)
Dec 24, 25 07:58 PM
10 Hard SAT Math Questions (Part - 41) -
ASTC Formula in Trigonometry
Dec 23, 25 11:34 PM
ASTC Formula in Trigonometry - Concepts - Examples and Solved Problems


