SOLVING POLYNOMIAL EQUATIONS BY FACTORING

The following steps will be useful to solve polynomial equations by factoring. 

Step 1 :

Make the right side of the equation zero (if it is not).

Step 2 : 

Factor the polynomial on the left side of the equation by grouping. 

Step 3 : 

Equate each factor to zero and solve for the variable.

Solved Examples

Example 1 :

Solve for x : 

x² – 5x + 6  =  0

Solution :

In the given quadratic equation, the coefficient of x² is 1.

Decompose the constant term +6 into two factors such that the product of the two factors is equal to +6 and the addition of two factors is equal to the coefficient of x, that is -5. 

Then, the two factors of +6 are 

-2 and -3

Factor the given quadratic equation using -2 and -3 and solve for x.

(x - 2)(x - 3)  =  0

x - 2  =  0  or  x - 3  =  0

x  =  2  or  x  =  3

So, the solution is {2, 3}. 

Example 2 :

Solve for x : 

3x² – 5x – 12  =  0

Solution :

In the given quadratic equation, the coefficient of x² is not 1.

So, multiply the coefficient of x² and the constant term "-12". 

3 ⋅ (-12)  =  -36

Decompose -36 into two factors such that the product of two factors is equal to -36 and the addition of two factors is equal to the coefficient of x, that is -5.

Then, the two factors of -36 are 

+4 and -9

Now we have to divide the two factors 4 and -9 by the coefficient of x², that is 3.

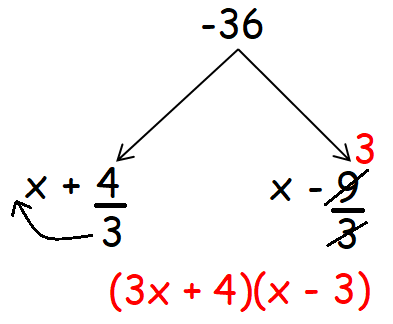
Now, factor the given quadratic equation and solve for x as shown below. 

(3x + 4)(x - 3)  =  0

3x + 4  =  0  or  x - 3  =  0

x  =  -4/3  or  x  =  3

So, the solution is {-4/3, 3}. 

Example 3 :

Solve for x :

(x + 3)²  =  25

Solution :

(x + 3)²  =  25

Subtract 25 from each side. 

(x + 3)² - 25  =  0

(x + 3)² - 5²  =  0

Using the algebraic identity a² - b²  =  (a + b)(a - b), factor the polynomial on the right side.  

[(x + 3) + 5][(x + 3) - 5]  =  0

[x + 3 + 5][x + 3 - 5]  =  0

(x + 8)(x - 2)  =  0

x + 8  =  0  or  x - 2  =  0

x  =  -8  or  x  =  2

So, the solution is {-8, 2}. 

Example 4 :

Solve for x : 

x³ + 3x² - 4x - 12  =  0

Solution :

x³ + 3x² - 4x - 12  =  0

Factor the polynomial on the left side of the equation by grouping. 

x²(x + 3) - 4(x + 3)  =  0

(x + 3)(x² - 4)  =  0

x + 3  =  0  or  x² - 4  =  0

So, the solution is {-3, -2, 2}. 

Example 5 :

Solve for x : 

3x³ + 5x² =  3x + 5

Solution :

3x³ + 5x² =  3x + 5

Subtract 3x and 5 from each side. 

3x³ + 5x² - 3x - 5  =  0

Factor the polynomial on the left side of the equation by grouping. 

x²(3x + 5) - 1(3x + 5)  =  0

(3x + 5)(x² - 1)  =  0

3x + 5  =  0  or  x² - 1  =  0

So, the solution is {-5/3, -1, 1}. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.