SOLVING PROBLEMS INVOLVING AREA

Let us recall the formula to find the area of a rectangle.

That is,

length × width

To find area of a rectangle, we multiply length and width. 

In case we know the area, and only one dimension, we can divide the area by the known dimension to find the other dimension.

The ultimate aim of this section is, how to solve problems using area. 

Solved Problems

Problem 1 : 

The area of a rectangular sandbox is 56 2/3 square feet. The length of the sandbox is 8 1/2 feet. What is the width ?

Solution :

We know the formula to find area of the rectangle.

That is, 

Area of the rectangle  =  length x width 

Plug the known values area and length and solve for the unknown value width.

56 2/3  =  8 1/2 x width 

170/3  =  17/2 x width

(170/3) x (2/17)  =  width

20/3  =  width

6 2/3  =  width

So, the width of the rectangle is 6 2/3 feet.

Problem 2 : 

The area of a circle is 154 square cm. Find its perimeter. 

Solution :

To find perimeter of the circle, we have to know the radius. 

So, we have to find the radius from the given area. 

We know the formula for area of circle.

That is,

Area of the circle  =  πr²

Substitute π  =  22/7, area  =  154. 

   154  =  22/7 x r² 

154 x 7/22  =  r²

49  =  r²

7²  =  r²

Perimeter of the circle  =  2πr

=  2x (22/7) x 7

=  2 x 22

=  44 cm

So, perimeter of the circle is 44 cm. 

Problem 3 : 

Mr. Webster is buying carpet for an exercise room where the basement of the room is in the shape of rectangle. The length and width of the room are 18 2/5 feet and 12 1/2 feet respectively. Find the total cost of the carpet, if the price of the carpet is $3 per square feet ?

Solution :

To know the total cost of the carpet, first we have to know the area of the basement.

Area of the basement  =  length x width

=  18 2/5 x 12 1/2

=  (92/5) x (25/2)

=  46 x 5

=  230 square feet

So, we need 230 square feet of carpet.

The cost each square feet of carpet  =  $3

Then, the cost of 230 square ft of carpet is

=  3 x 230

=  $690

So, the total cost of the carpet is $690.

Problem 4 : 

If the area of a square is 64 square inches, find the length of its diagonal. 

Solution :

Let 'a' be the length of one side of the square. 

We all know the formula for area of square.

That is,

Area of square  =  side x side  =  a²

64  =  a²

8²  =  a²

8  =  a

So, the length of side of the square is 8 inches.

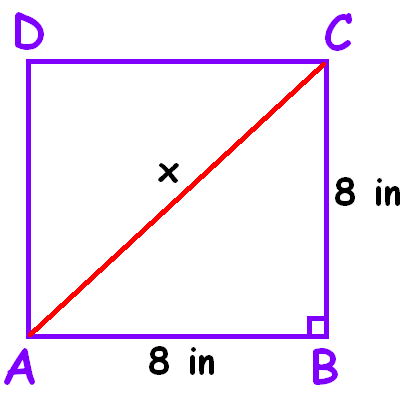
In the above picture, we have to find the length of AC, say 'x'. 

Using Pythagorean theorem in the right triangle ABC, we get

AC>²  =  AB² + BC²

x²  =  8² + 8²

x²  =  64 + 64

x²  =  128

Take square root on both sides. 

√x²  =  √128

x  =  √(2x64)

x  =  8√2 inches

The length of its diagonal is 8√2 inches.

Problem 5 : 

If the radii of two circles are in the ratio 2 : 3, then find the ratio between their areas.  

Solution :

From, the given information, we have

Radius of the first circle  =  2x

Radius of the second circle  =  3x

Area of the first circle  =  πr²  =  π(2x)²  =  4πx²

Area of the second circle  =  πr²  =  π(3x)²  =  9πx²

Ratio between their areas is 

=  4πx² : 9πx²

=  4 : 9

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.