SOLVING PROBLEMS USING LAGRANGES MEAN VALUE THEOREM

Let f (x) be continuous in a closed interval [a, b] and differentiable in the open interval (a, b) (where f (a), f (b) are not necessarily equal). Then there exist at least one point c ∈ (a, b) such that,

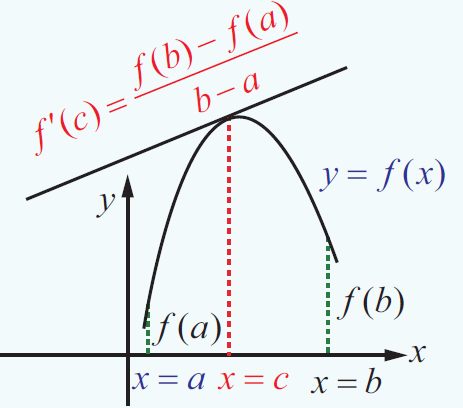
A geometrical meaning of the Lagrange’s mean value theorem is that the instantaneous rate of change at some interior point is equal to the average rate of change over the entire interval.

Problem 1 :

Explain why Lagrange’s mean value theorem is not applicable to the following functions in the respective intervals :

(i)  f(x)  =  (x+1)/x, x ∊ [-1, 2]

Solution :

The function is not continuous on the interval [-1, 2].

(ii)  f(x)  =  |3x+1|, x ∊ [-1, 3]

Solution :

The function is defined and continuous on [-1, 3],

f'(x)  =  (3x+1) / |3x+1|

it is not differentiable at x  =  -1/3

Problem 2 :

Using the Lagrange’s mean value theorem determine the values of x at which the tangent is parallel to the secant line at the end points of the given interval:

(i)  f (x)  =  x³ - 3x + 2, x ∊ [-2, 2]

Solution :

The function is defined and continuous on [-2, 2], it is differentiable on (-2, 2).

f'(x)  =  3x²-3

f(-2)  =  (-2)³ - 3(-2) + 2

=  -8 + 6 + 2

=  0

f(2)  =  2³ - 3(2) + 2

=  8 - 6 + 2

=  4

f'(x)  =  [f(b)-f(a)]/(b-a)

3x²-3  =  (4-0) / (2+2)

3x²-3  =  1

3x²  =  4

x  =  ±2/√3

(ii)  f(x)  =  (x-2)(x-7),  x ∊ [3, 11]

Solution :

f(x)  =  (x-2)(x-7)

The function is defined and continuous on [3, 11], and differentiable on (3, 11).

u  =  x - 2  v  =  x - 7

u'  =  1 and v'  =  1

f'(x)  =  (x-2)(1) + 1(x-7)

f'(x)  =  x-2+x-7  ===>  2x-9

f'(x)  =  [f(b) - f(a)] / (b-a)

2x-9  =  (-4-36)/(3-11)

2x-9  =  -40/(-8)

2x-9  =  5

2x  =  14

x  =  14/2

x  =  7∊ [3, 11]

Problem 3 :

Show that the value in the conclusion of the mean value theorem for

(i) f (x) = 1/x

on a closed interval of positive numbers [a, b] is √ab

f'(x)  =  -1/x²

f(a)  =  1/a and f(b)  =  1/b

f'(x)  =  [f(b) - f(a)]/(b-a)

-1/x²  =  [(1/b) - (1/a)]/(b-a)

-1/x²  =  [(a-b)/ab]/(b-a)

-1/x²  =  -1/ab

x2  =  ab

x  =  √ab

(ii) f (x) = Ax² + Bx + C on any interval [a, b] is (a + b)/2

Solution :

f (x) = Ax² + Bx + C

f'(x)  =  2Ax + B

 f (b) = Ab² + Bb + C

 f (a) = Aa² + Ba + C

f(b) - f(a)  =  (Ab² + Bb) - (Aa² + Ba)

=  A(b²-a²) + B(b-a)

=  (b-a) [A(b+a) + B]

f'(x)  =  (b-a) [A(b+a) + B] / (b-a)

2Ax + B  =  Ab+Aa + B

2Ax  =  Ab+Aa+B-B

x  =  (Ab+Aa) / 2A 

x  =  (a+b)/2

Problem 4 :

Determine whether

f(x) = cos x - sin x

satisfies the MVT on the interval [π/4, 5π/4] if it does, find all numbers c in (π/4, 5π/4) such that f'(c) = f(b) - f(a) / (b - a)

Solution :

Given that, f(x) = cos x - sin x

f'(x) = -sin x - cos x

f(a) = f(π/4) = cos π/4 - sin π/4

= √2/2 - √2/2

= 0

f(b) = f(5π/4) = cos 5π/4 - sin 5π/4

= cos (π + (π/4)) - sin (π + (π/4)) 

= cos (π/4) + sin (π/4)

= -√2/2 + √2/2  

= 0

f'(c) = f(b) - f(a) / (b - a)

-sin c - cos c = 0

-sin c = cos c

-sin c / cos c = 1

tan c = -1

c = tan^-1(-1)

c = 3π/4

So, the required value of c is 3π/4.

Decide whether mean value theorem applies. If it applies, find the value of x that satisfy the theorem. 

Problem 5 :

f(x) = (x + 3) / (x - 3); [-1, 4]

Solution :

i) The function f(x) is not continuous at x = 3. So, mean value theorem cannot be applied.

Problem 6 :

f(x) = (1/3)x³ + (1/3)x - 4/3; [-1, 2]

Solution :

f(x) = (1/3)x³ + (1/3)x - 4/3

i) The function f(x) is continuous in the on the closed interval [-1, 2].

(ii) f(x) = (1/3)x³ + (1/3)x - 4/3

f'(x) = (1/3)(3x²) + (1/3)(1) - 0

= x² + (1/3)

The function is differentiable in the open interval (-1, 2).

f'(c) = c² + (1/3)

f(b) = f(2) = (1/3)2³ + (1/3)2 - 4/3

= 8/3 + 2/3 - 4/3

= 2

f(a) = f(-1) = (1/3)(-1)³ + (1/3)(-1) - 4/3

= -1/3 - 1/3 - 4/3

= -2

f'(c) = f(b) - f(a) / (b - a)

c² + (1/3) = [2 - (-2)]/(2 + 1)

c² + (1/3) = 4/3

c² = (4/3) - (1/3)

c² = (3/3)

c = -1 and 1

So, the required value of c lies in the given interval is 1.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.