SOLVING QUADRATIC EQUATIONS BY FACTORING USING BOX METHOD

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

Factoring Quadratic Expressions Using Box Method - Steps

Step 1 :

Draw a box, split it into four parts.

Write the first and last term in the first and last box respectively.

Step 2 :

We have to multiply the coefficient of x² term and constant term.

Now, we have to decompose the value that we get in step 2, such that the product must be equal to the value in step 2 and simplified value must be equal to the middle term.

Step 3 :

Write those values in the empty boxes. Factor horizontally and vertically

Step 4 :

Write the horizontal and vertical terms as pairs. By equating each factor to zero, we will get the values of x.

Solved Examples

Example 1 :

Solve the following quadratic equation :

x² - 3x - 10 = 0

Solution :

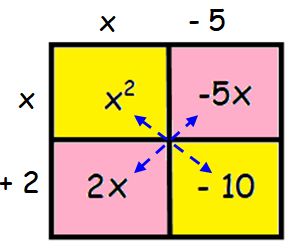
From the box method, we find the factors.

The factors are (x + 2) and (x - 5).

Then,

(x + 2)(x - 5) = 0

x + 2 = 0

x = -2

x - 5 = 0

x = 5

So, the solutions is {-2, 5}.

Example 2 :

Solve the following quadratic equation :

2x² + x - 6 = 0

Solution :

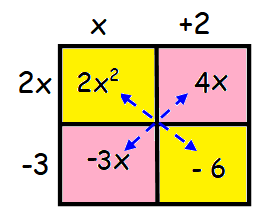
From the box method, we find the factors.

The factors are (2x - 3) and (x + 2).

Then,

(2x - 3)(x + 2) = 0

2x - 3 = 0

2x = 3

x = 3/2

x + 2 = 0

x = -2

So, the solution is {3/2, -2}.

Example 3 :

Solve the following quadratic equation :

√2x² + 7x + 5√2 = 0

Solution :

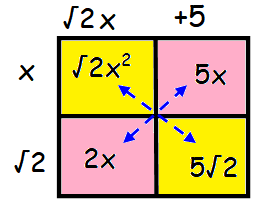
From the box method, we find the factors.

The factors are (x + √2) and (√2x + 5).

Then,

(x + √2)(√2x + 5) = 0

x + √2 = 0

x = -√2

√2x + 5 = 0

√2x = -5

x = -5/√2

So, the solution is {-√2, -5/√2}.

Example 4 :

Solve the following quadratic equation :

2x² - x + (1/8) = 0

Solution :

In the above quadratic equation, multiply each side by 8.

16x²- 8 x + 1 = 0

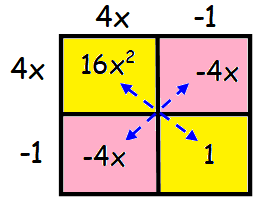
From the box method, we find the factors.

The factors are (4x - 1) and (4x - 1).

Then,

(4x - 1)(4x - 1) = 0

4x - 1 = 0

4x = 1

x = 1/4

4x - 1 = 0

4x = 1

x = 1/4

So, the solutions {1/4, 1/4}.

Example 5 :

Solve the following quadratic equation :

100x² - 20 x + 1 = 0

Solution :

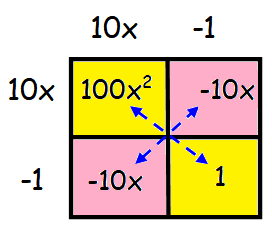
From the box method, we find the factors.

The factors are (10x - 1) and (10x - 1).

Then,

(10x - 1)(10x - 1) = 0

10x - 1 = 0

10x = 1

x = 1/10

10x - 1 = 0

10x = 1

x = 1/10

So, the solution is {1/10, 1/10}.

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

About Us | Contact Us | Privacy Policy

SOLVING QUADRATIC EQUATIONS BY FACTORING USING BOX METHOD

Factoring Quadratic Expressions Using Box Method - Steps

Solved Examples

Recent Articles

AP Calculus BC Problems with Solutions

AP Precalculus Problems and Solutions (Part - 1)

AP Calculus AB Problems with Solutions (Part - 1)