SOLVING QUADRATIC EQUATIONS BY GRAPHING
First, we have to draw the graph for the given quadratic equation. To solve the second quadratic equation using the first, we have to subtract the second equation from the first equation. So we get a straight line.
We can determine roots of a quadratic equation graphically by choosing appropriate parabola and intersecting it with a desired straight line.
(i) If the straight line intersects the parabola at two distinct points, then the x coordinates of those points will be the roots of the given quadratic equation.
(ii) If the straight line just touch the parabola at only one point, then the x coordinate of the common point will be the single root of the quadratic equation.
(iii) If the straight line doesn’t intersect or touch the parabola then the quadratic equation will have no real roots.
Solved Questions
Question 1 :
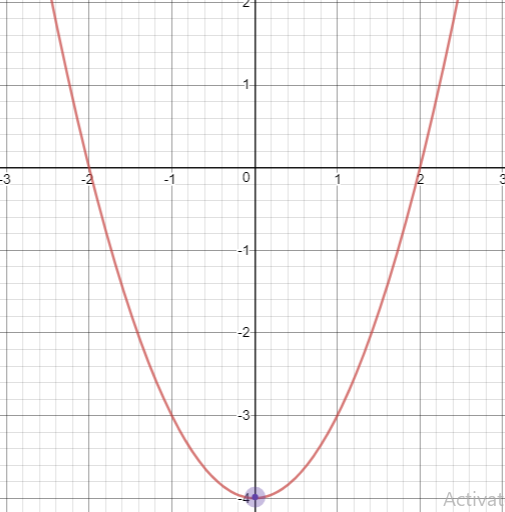
Draw the graph of y = x2−4 and hence solve x2−x −12 = 0
Solution :
Now, let us draw the graph of y = x2−4
|
x -4 -3 -2 -1 0 1 2 3 4 |
x2 16 9 4 1 0 1 4 9 16 |
-4 -4 -4 -4 -4 -4 -4 -4 -4 -4 |
y 12 5 0 -3 -4 -3 0 5 12 |
Points to be plotted :
(-4, 12) (-3, 5) (-2, 0) (-1, -3) (0, -4) (1, -3) (2, 0) (3, 5) (4, 12)
To find the x-coordinate of the vertex of the parabola, we may use the formula x = -b/2a
x = 0/2(2) = 0
By applying x = 0, we get the value of y.
y = 02 - 4
y = -4
Vertex (0, -4)
y = x2−4 ------(1)
0 = x2−x −12 ------(2)
(1) - (2)
y = x2 − 4
0 = x2−x −12
(-) (-) (+) (+)
-----------------
y = x + 8
Now let us draw a graph for the line
|
x -3 -2 -1 0 1 2 3 |
x -3 -2 -1 0 1 2 3 |
+8 +8 +8 +8 +8 +8 +8 +8 |
y 5 6 7 8 9 10 11 |
Points on line :
(-3, 5) (-2, 6) (-1, 7) (0, 8) (1, 9) (2, 10) (3, 11)
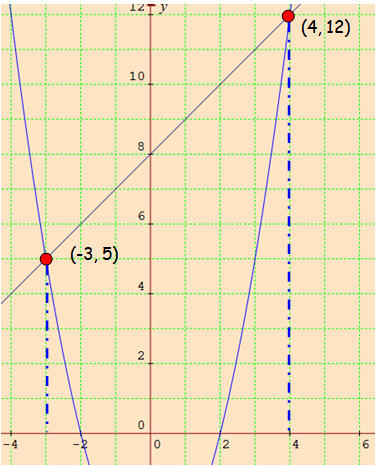
The parabola and a line intersect at two points (-3, 5) and (4, 12).
Hence the solutions are -3 and 4.
Question 2 :
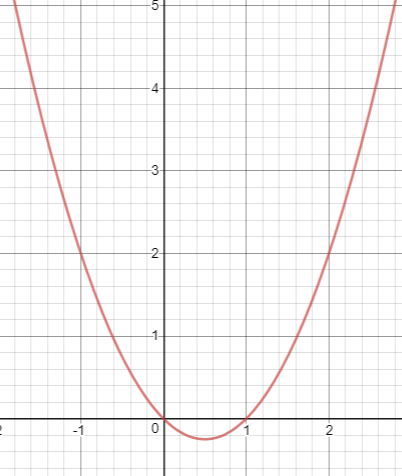
Draw the graph of y = x2 + x and hence solve x2 + 1 = 0
Solution :
Now, let us draw the graph of y = x2 + x
|
x -4 -3 -2 -1 0 1 2 3 4 |
x2 16 9 4 1 0 1 4 9 16 |
+x -4 -3 -2 -1 0 1 2 3 4 |
y 12 6 2 0 0 2 6 12 20 |
Points to be plotted :
(-4, 12) (-3, 6) (-2, 2) (-1, 0) (0, 0) (1, 2) (2, 6) (3, 12) (4, 20)
To find the x-coordinate of the vertex of the parabola, we may use the formula x = -b/2a
x = 1/2(1) = 1/2
By applying x = 1/2, we get the value of y.
y = (1/2)2 + (1/2)
= (1/4) + (1/2)
= (1 + 2)/4
= 3/4
Vertex (1/2, 3/4)
y = x2 + x ------(1)
0 = x2 + 1 ------(2)
(1) - (2)
y = x2 + x
0 = x2 + 1
(-) (-) (-)
-----------------
y = x - 1
Now let us draw a graph for the line
Points on line :
(-3, -4) (-2, -3) (-1, -2) (0, -1) (1, 0) (2, 1) (3, 2)
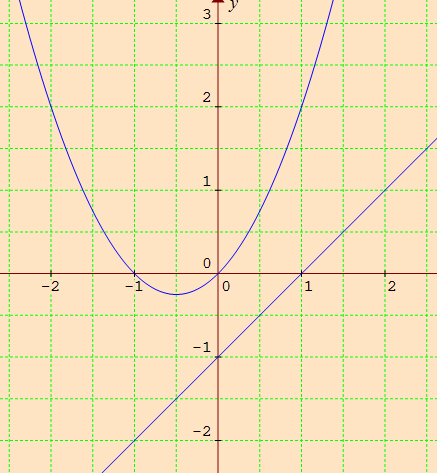
The parabola and a line do not intersect at anyware. So it has no real roots.
Question 3 :
Draw the graph of y = x2 + 3x + 2 and use it to solve x2 + 2x + 1 = 0.
Solution :
Now let us draw the graph of y = x2 + 3x + 2
|
x -4 -3 -2 -1 0 1 2 3 4 |
x2 16 9 4 1 0 1 4 9 16 |
+3x -12 -9 -6 -3 0 3 6 9 12 |
+2 +2 +2 +2 +2 +2 +2 +2 +2 +2 |
y 6 2 0 0 2 6 12 20 30 |
Points to be plotted :
(-4, 6) (-3, 2) (-2, 0) (-1, 0) (0, 2) (1, 6) (2, 12) (3, 20) (4, 30)
To find the x-coordinate of the vertex of the parabola, we may use the formula x = -b/2a
x = -3/2(1) = -3/2
By applying x = -3/2, we get the value of y.
y = x2 + 3x + 2
= (-3/2)2 + 3(-3/2) + 2
= (9/4) - (9/4) + 2
= 2
Vertex (-3/2, 2)
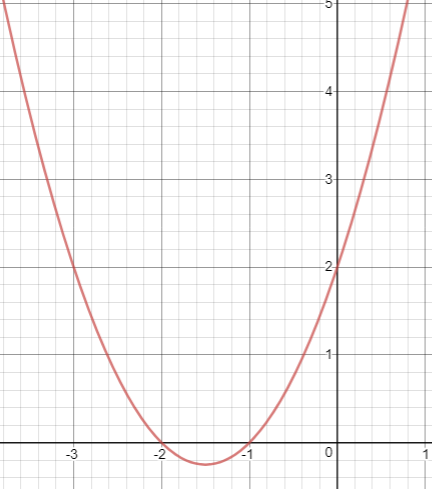
y = x2 + 3x + 2 ------(1)
0 = x2 + 2x + 1 ------(2)
(1) - (2)
y = x2 + 3x + 2
0 = x2 + 2x + 1
(-) (-) (-) (-)
--------------------
y = x + 1
Now let us draw a graph for the line
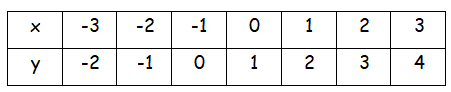
points on the line :
(-3, -2) (-2, -1) (-1, 0) (0, 1) (1, 2) (2, 3) (3, 4)
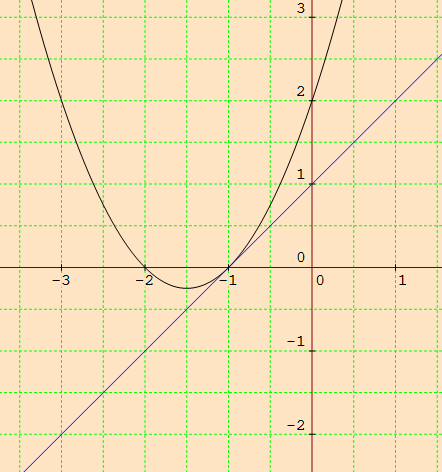
The line and the parabola intersects at one point, that is -1.
Hence -1 is the solution.
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
De Moivre's Theorem and Its Applications
Apr 19, 24 08:30 AM
De Moivre's Theorem and Its Applications -
First Fundamental Theorem of Calculus - Part 1
Apr 17, 24 11:27 PM
First Fundamental Theorem of Calculus - Part 1 -
Polar Form of a Complex Number
Apr 16, 24 09:28 AM
Polar Form of a Complex Number
