SOLVING QUADRATIC  INEQUALITIES GRAPHICALLY

The following steps will be useful to solve quadratic inequalities graphically.

Step 1 :

Let the given quadratic inequality be 

ax² + bx + c ≥ 0

We have to write the quadratic function

y  =  ax² + bx + c

Step 2 :

The graph of y  =  ax² + bx + c will either be open upward or downward parabola. 

We can use the below table to know whether it is open upward or down ward.  

Step 3 :

The graph of  y = ax² + bx + c may intersect x- axis or not.

We can use the below table to know whether it intersects x -axis or not.

Step 4 :

We can use the formula

x = -b / 2a

and find the vertex of the parabola. 

Step 5 :

We can use the results of step 2, step 3, step 4 and sketch the graph of the given parabola.

Step 6 :

We can get solution for the given inequality from the graph of the parabola.

Example 1 :

Solve the quadratic inequality given below graphically.

x² + 5x + 6 ≥ 0

Solution :

Step 1 :

Let

y  =  x² + 5x + 6 -----(1)

Then we have,

x² + 5x + 6 ≥ 0 -----> y ≥ 0

Step 2 :

The sign of x² is positive. So the parabola is open upward.

Step 3 :

b² - 4ac  =  (5)² - 4(1)(6)

b² - 4ac  =  25 - 24

b² - 4ac  =  1 ≥ 0

So, the parabola intersects x - axis.

Step 4 :

To find x co-ordinate of the vertex, use the formula

x  =  -b / 2a

Substitute 5 for b and 1 for a.

x  =  -b / 2a

x  =  -5 / 2(1)

x  =  -5 / 2

x  =  -2.5

Substitute -2.5 for x in (1)

(1)-----> y  =  (-2.5)² + 5(-2.5) + 6

y  =  6.25 - 12.5 + 6

y  =  -0.245

Therefore, the vertex is (-2.5, -0.25)

Step 5 :

We can use the results of step 2, step 3, step 4 and sketch the parabola. 

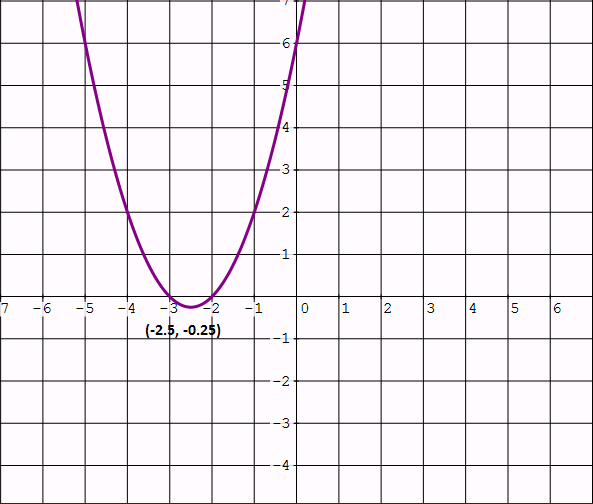
Step 6 :

The given inequality is,  

x² + 5x + 6 ≥ 0

y ≥ 0 -----> (y is positive)

When we look at the above graph, y is positive in the intervals 

(-∞, -3] &  [-2,+∞) of x

Hence, the solution is, 

(-∞, -3] U [-2,+∞)

Example 2 :

Solve the quadratic inequality given below graphically.

-x² + 2x - 5 ≤ 0

Solution :

Step 1 :

Let

y  =  -x² + 2x - 5

Then, we have 

-x² + 2x - 5 ≤ 0 -----> y ≤ 0

Step 2 :

The sign of x² is negative. So the parabola is open downward.

Step 3 :

b² - 4ac  =  (2)² - 4(-1)(-5)

b² - 4ac  =  4 - 20

b² - 4ac  =  -16 < 0

So, the parabola does not intersects x - axis.

Step 4 :

To find x co-ordinate of the vertex, use the formula

x  =  -b / 2a

Substitute 2 for b and -1 for a. 

x  =  -2/2(-1)

x  =  -2/(-2)

x  =  1

Substitute 1 for x in (1). 

(1)-----> y  =  -(1)² + 2(1) - 5

y  =  -1 + 2 - 5

y  =  -4

Therefore, the vertex is (1, -4).

Step 5 :

We can use the results of step 2, step 3, step 4 and sketch the parabola. 

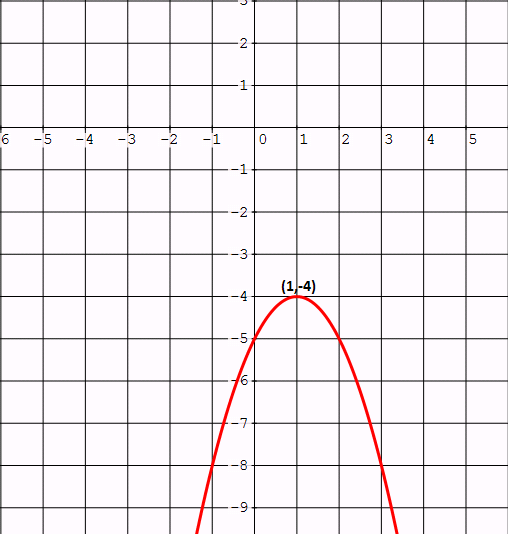
Step 6 :

The given inequality is,  

-x² + 2x - 5 ≤ 0

y ≤ 0 -----> (y is negative)

When we look at the above graph, y is negative for all real values of x. 

Hence, the solution is, 

All real values  (or) x ∈ R

Example 3 :

Solve the quadratic inequality given below graphically.

-x² + 4 ≥ 0

Solution :

Step 1 :

Let

y  =  -x² + 4 -----(1)

Then we have, 

-x² + 4 ≥ 0 -----> y ≥ 0

Step 2 :

The sign of x² is negative. So the parabola is open downward.

Step 3 :

b² - 4ac  =  (0)² - 4(-1)(4)

b² - 4ac  =  0 + 16

b² - 4ac  =  16 ≥ 0

So, the parabola intersects x - axis.

Step 4 :

To find x co-ordinate of the vertex, use the formula

x  =  -b / 2a

Substitute 0 for b and -1 for a.

x  =  0 / 2(-1)

x  =  0

Substitute 0 for x in (1)

(1)-----> y  =  -(0)² + 4

y  =  0 + 4

y  =  4

Therefore, the vertex is (0, 4).

Step 5 :

We can use the results of step 2, step 3, step 4 and sketch the parabola. 

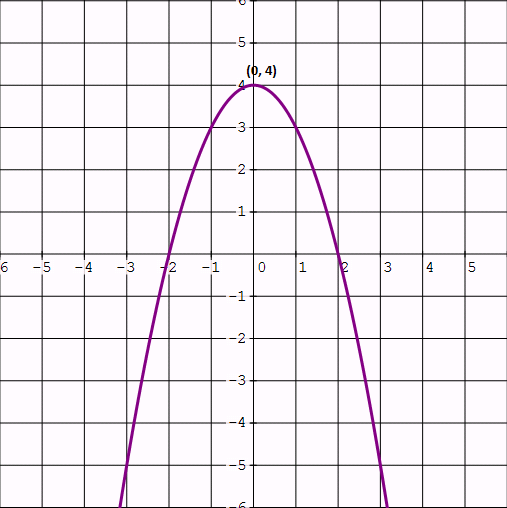
Step 6 :

The given inequality is,  

-x² + 4 ≥ 0 -----> y ≥ 0 -----> (y is positive)

When we look at the above graph, y is positive in the interval [-2, 2] of x. 

Hence the solution is, 

[-2, 2]

Example 4 :

Solve the quadratic inequality given below graphically.

x² + 4x +7 ≤ 0

Solution :

Step 1 :

Let

y  =  x² + 4x +7 -----(1)

Then we have, 

x² + 4x +7 ≤ 0 -----> y ≤ 0

Step 2 :

The sign of x² is positive. So the parabola is open upward.

Step 3 :

b² - 4ac  =  (4)² - 4(1)(7)

b² - 4ac  =  16 - 28

b² - 4ac  =  -12 

So, the parabola does not intersects x - axis.

Step 4 :

To find x co-ordinate of the vertex, use the formula

x  =  -b / 2a

Substitute 4 for b and 1 for a.

x  =  -4 / 2(1)

x  =  -4 / 2

x  =  -2

Substitute -2 for x in (1).

(1)-----> y  =  (-2)² + 4(-2) + 7

y  =  4 - 8 + 7

y  =  3

Therefore, the vertex is (-2, 3).

Step 5 :

We can use the results of step 2, step 3, step 4 and sketch the parabola. 

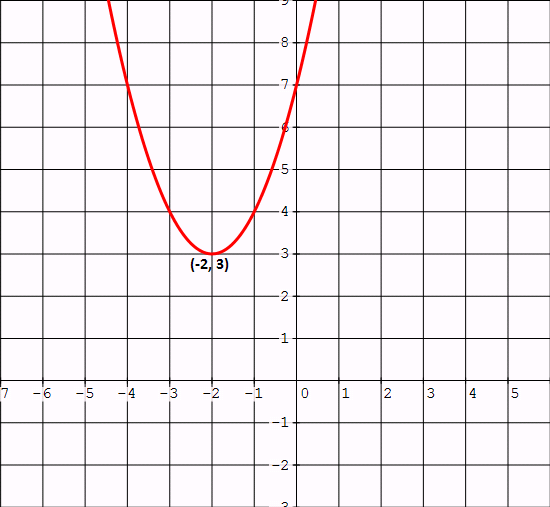
Step 6 :

The given inequality is,  

x² + 4x +7 ≤ 0 -----> y ≤ 0 (y is negative)

When we look at the above graph, y is positive for all real values of x.  

It contradicts the given inequality.

Hence, there is no solution.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.