SOLVING RATIONAL INEQUALITIES EXAMPLES

Solve for  x :

Example 1 :

(x + 2)/(x – 3) < 0

Solution :

Let f(x)  =  (x + 2)/(x – 3)

f(x) < 0

(x + 2)/(x – 3) < 0

By equating the numerator and denominator to zero, we get

x + 2  =  0, x – 3  =  0

x  =  -2 and x  =  3 (critical numbers)

The critical numbers are dividing the number line into three intervals.

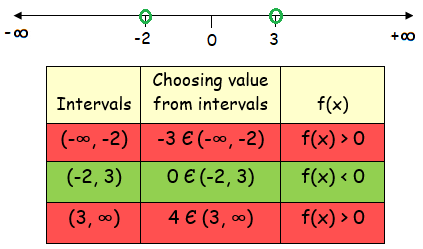
From the table, the possible values of x are

-2 < x < 3

By writing it as interval notation, we get

(-2, 3)

So, the required solution is -2 < x < 3

Example 2 :

(x + 3)/(2 – x) < 0

Solution :

Let f(x)  =  (x + 3)/(2 – x)

f(x) < 0

(x + 3)/(2 – x) < 0

By equating the numerator and denominator to zero, we get

x + 3  =  0, 2 – x  =  0

x  =  -3 and x  =  2 (critical numbers)

The critical numbers are dividing the number line into three intervals. 

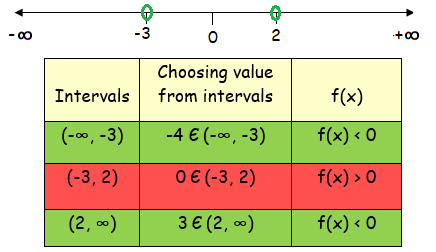
From the table, the possible values of x are

x < -3 or x > 2

By writing it as interval notation, we get

(-∞, -3) u (2, ∞)

So, the required solution is x < -3 or x > 2

Example 3 :

(x - 1)/(x + 3) ≥ -1

Solution :

Let f(x)  =  (x - 1)/(x + 3)

f(x) ≥ -1

(x - 1)/(x + 3) ≥ -1

Add 1 on both sides, we get

(x - 1)/(x + 3) + 1 ≥ -1 + 1

Taking least common multiple, we get

[(x – 1) + (x + 3)]/(x + 3) ≥ 0

(x - 1 + x + 3)/(x + 3) ≥ 0

(2x + 2)/(x + 3) ≥ 0

By equating the numerator and denominator to zero, we get

2x + 2  =  0, x + 3  =  0

x  =  -1 and x  =  -3 (critical numbers)

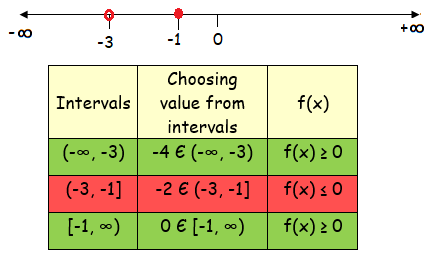
From the table, the possible values of x are

x < -3 or x ≥ -1

By writing it as interval notation, we get

(-∞, -3) u [-1, ∞)

So, the required solution is x < -3 or x ≥ -1

Example 4 :

(x + 2)/(2x - 3) < 1

Solution :

(x + 2)/(2x - 3) < 1

Subtract 1 on both sides, we get

(x + 2)/(2x - 3) - 1 < 1 – 1

(x + 2)/(2x - 3) - 1 < 0

Taking least common multiple, we get

[(x + 2) + (-2x + 3)]/(2x - 3) < 0

(x + 2 - 2x + 3)/(2x - 3) < 0

-(x - 5)/(2x - 3) < 0

Make a coefficient x as positive, so we have to multiply by -1 through out the equation,

(x - 5)/(2x - 3) > 0

By equating the numerator and denominator to zero, we get

x - 5  =  0, 2x - 3  =  0

x  =  5 and x  =  3/2 (critical numbers)

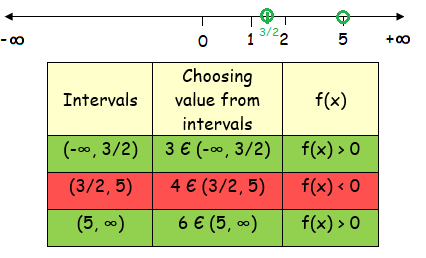
From the table, the possible values of x are

x < 3/2 or x > 5

By writing it as interval notation, we get

(-∞, 3/2) u (5, ∞)

So, the required solution is x < 3/2 or x > 5

Example 5 :

(5 – 2x)/(1 - x) > 4

Solution :

(5 – 2x)/(1 - x) > 4

Subtract 4 on both sides, we get

(5 – 2x)/(1 - x) - 4 > 4 – 4

(5 – 2x)/(1 - x) - 4 > 0

Taking least common multiple, we get

[(5 – 2x) - 4(1 - x)]/(1 - x) > 0

(5 – 2x - 4 + 4x)/(1 - x) > 0

(2x + 1)/(1 - x) > 0

By equating the numerator and denominator to zero, we get

2x + 1  =  0, 1 - x  =  0

x  =  -1/2 and x  =  1 (critical numbers)

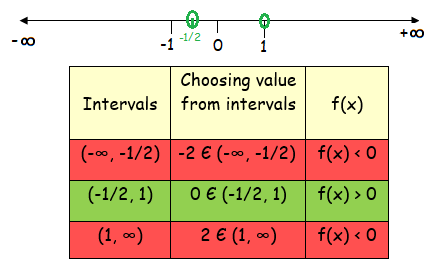
From the table, the possible values of x are

-1/2 < x < 1

By writing it as interval notation, we get

(-1/2, 1)

So, the required solution is -1/2 < x < 1.

Example 6 :

(x - 1)/(x + 2) ≤ 0

Solution :

(x - 1)/(x + 2) ≤ 0

Equating the denominator to 0, we get

x = -2

x - 1 = 0

x = 1

(-∞, -2) (-2, 1) and (1, ∞)

So, the solution is -2< x ≤ 1.

Example 7 :

[(2x - 3)/(x + 5)] ≥ [(2x + 7)/(x - 3)]

Solution :

[(2x - 3)/(x + 5)] ≥ [(2x + 7)/(x - 3)]

[(2x - 3)/(x + 5)] - [(2x + 7)/(x - 3)] ≥ 0

[(2x - 3)(x - 3) - (2x + 7)(x + 5)]/(x + 5)(x - 3) ≥ 0

(2x² - 9x + 9) - (2x² + 17x + 35)/(x + 5)(x - 3) ≥ 0

(-26x - 26) / (x + 5)(x - 3) ≥ 0

-26 (x + 1) / (x + 5)(x - 3) ≥ 0

26 (x + 1) / (x + 5)(x - 3) ≤ 0

Zeroes are -5 and 3.

Equating the numerator to 0, we get x = -1

(-∞, -5) (-5, -1) (1, 3) and (3, ∞).

So, the solution is (-∞, -5) U (1, 3).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.