SOLVING SYSTEM OF EQUATIONS

We can use one of the following methods to solve a system of linear equations. 

1. Elimination Method

2. Substitution Method

3. Cross Multiplication Method 

4. Graphing

Solved Examples

Example 1 :

Solve by elimination method. 

3x + 4y  =  7

x - 4y  =  -3

Solution :

3x + 4y  =  7 -----(1)

x - 4y  =  -3  -----(2)

In the given two equations, y-term has the same coefficient and different signs. By adding the above two equations, we can eliminate y-term and solve for y. 

(1) + (2) : 

4x  =  4

Divide each side by 4.

x  =  1

Substitute x  =  1 in (1). 

3(1) + 4y  =  7

3 + 4y  =  7 

Subtract 3 from each side. 

4y  =  4

Divide each side by 4.

y  =  1

So, the solution is 

(x, y)  =  (1, 1)

Example 2 :

Solve by elimination method. 

3x + 4y  =  -25

2x - 3y  =  6

Solution :

3x + 4y  =  -25 -----(1)

2x - 3y  =  6  -----(2)

Both x terms and y terms have different coefficients in the above system of equations.

Let's try to make the coefficients of y terms equal.

To make the coefficients of y terms equal, we have to find the least common multiple 4 and 3.

The least common multiple of 4 and 3 is 12.

Multiply the first equation by 3 in order to make the coefficient of y as 12 and multiply the second equation by 4 in order to make the coefficient of y as -12. 

(1) ⋅ 3 ---->  9x + 12y  =  -75

(2) ⋅ 4 ---->  8x - 12y  =  24

Now, we can add the two equations and eliminate y as shown below. 

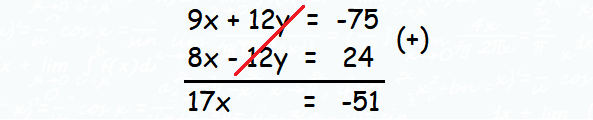
Divide each side by 17. 

x  =  -3

Substitute -3 for x in (1). 

(1)---->  3(-3) + 4y  =  -25

-9 + 4y  =  -25

Add 9 to each side.

4y  =  -16

Divide each side by 4.

y  =  -4

So, the solution is

(x, y)  =  (-3, -4)

Example 3 : 

Solve for x and y using substitution. 

x - 5y + 17  =  0

2x + y + 1  =  0

Solution : 

x - 5y + 17  =  0 -----(1)

2x + y + 1  =  0 -----(2)

Step 1 :

Solve (1) for x. 

x - 5y + 17  =  0

Subtract 17 from each side. 

x - 5y  =  -17

Add 5y to each side.

x  =  5y - 17 -----(3)

Step 2 : 

Substitute (5y - 17) for x into (2). 

(2)-----> 2(5y - 17) + y + 1  =  0

10y - 34 + y + 1  =  0

11y - 33  =  0

Add 33 to each side.

11y  =  33

Divide each side by 11.

y  =  3

Step 3 :

Substitute 3 for y into (3).

(3)-----> x  =  5(3) - 17

x  =  15 - 17

x  =  -2

So, the solution is 

(x, y)  =  (-2, 3)

Example 4 :

Solve the following system of equations using cross multiplication method.

2x + 7y - 5  =  0

-3x + 8y  =  -11

Solution:

First we have to change the given linear equations in the form a₁x + b₁y + c₁  =  0, a₂x + b₂y + c₂  =  0.

2x + 7y - 5  =  0

-3x + 8y + 11  =  0

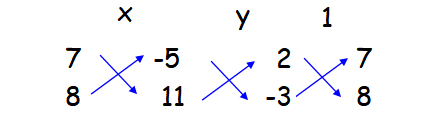
x/(77 + 40)  =  y/(15 - 22)  =  1/[16 + 21]

x/117  =  y/(-7)  =  1/37

So, the solution is

(x, y)  =  (117/37, -7/37)

Example 5 :

Solve the following system of equations by graphing.

x + y - 4  =  0 

3x - y  =  0

Solution :

Step 1 :

Let us re-write the given equations in slope-intercept form  (y = mx + b). 

y  =  - x + 4

(slope is -1 and y-intercept is 4) 

y  =  3x 

(slope is 3 and y-intercept is 0) 

Based on slope and y-intercept, we can graph the given equations. 

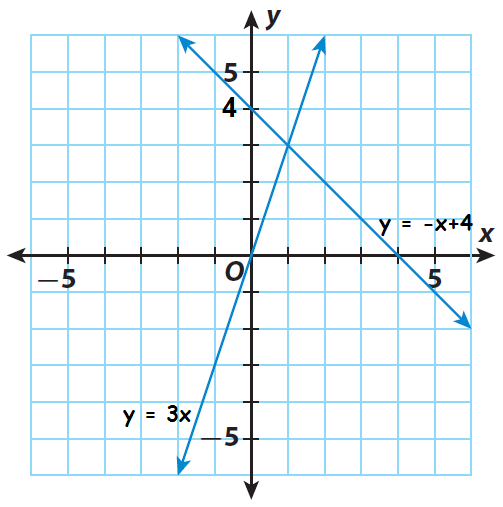
Step 2 :

Find the point of intersection of the two lines. It appears to be (1, 3). Substitute to check if it is a solution of both equations.

Because the point (1, 3) satisfies both the equations, the solution for the given system is (1, 3).  

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.