SOLVING SYSTEMS BY ELIMINATION WITH MULTIPLICATION

In some linear systems, neither variable can be eliminated by adding or subtracting the equations directly.

In systems like these, you need to multiply one of the equations by a constant so that adding or subtracting the equations will eliminate one variable. 

Solved Examples

Problem 1 :

Solve the system of equations by multiplying and adding.

3x - 5y  =  -17

2x + 15y  =  7

Solution :

Step 1 :

Let us eliminate the variable y in the given two equations. 

3x - 5y  =  -17 -------- (1)

2x + 15y  =  7 -------- (2)

Step 2 :

To make the coefficient of y same in both the equations, multiply the first equation by 3.  

(1) ⋅ 3 ----- > 9x - 15y  =  -51 -------- (3)

In equations (2) and (3), the variable y is having the same coefficient, but having different signs.

Step 3 :

Add the equations (2) and (3) to eliminate the variable y. 

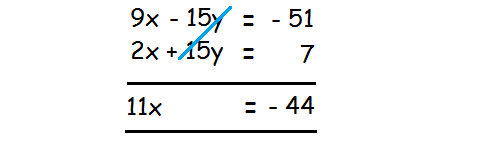
Divide both sides by 11.

11x / 11  =  - 44 / 11

x  =  - 4

Step 4 : 

Substitute the value of x into one of the equations to find the value of y. 

3x - 5y  =  -17

3(-4) - 5y  =  -17

-12 - 5y  =  -17

Add 12 to both sides.

(-12 - 5y) + 12  =  (-17) + 12

-12 - 5y + 12  =  -17 + 12

Simplify.

-5y  =  -5

Divide both sides by -5

-5y / (-5)  =  -5 / (-5)

y  =  1

Hence, the solution to the system is

(x, y)  =  (-4, 1)

Problem 2 :

Contestants in the Run-and-Bike-a-thon run for a specified length of time, then bike for a specified length of time. Jacob ran at an average speed of 5.2 mi/h and biked at an average speed of 20.6 mi/h, going a total of 14.2 miles. Alex ran at an average speed of 10.4 mi/h and biked at an average speed of 18.4 mi/h, going a total of 17 miles. For how long do contestants run and for how long do they bike ?

Solution :

Step 1 :

Let the contestants run "x" hours and bike "y" hours.

Using the formula, Distance  =  Speed x Time, 

Jacob :  5.2x + 20.6y  =  14.2  

Alex :  10.4x + 18.4y  =  17

Step 2 :

In both the equations we have decimal. In the terms we have decimal, the maximum number of digits after the decimal is 1. 

So multiply both the equations by 10.

10(5.2x + 20.6y)  =  10(14.2)  

52x + 206y  =  142 -------- (1)

10(10.4x + 18.4y)10  =  10(17)

104x + 184y  =  170 -------- (2)

Step 3 : 

Eliminate one of the variables to get the value of the other variable.

In (1) and (2), both the variables "x" and "y" are not having the same coefficient.

One of the variables must have the same coefficient. 

So multiply both sides of (1) by 2 to make the coefficients of "x" same in both the equations.  

(1) ⋅ 2 -------->  104x + 412y  =  284 ----------(3) 

Variable "x" is having the same sign in both (1) and (2). 

To change the sign of "x" in (3), multiply both sides of (2) by negative sign.

- (104x + 412y)  =  - 284

- 104x - 412y  =  - 284 --------(4)

Step 4 : 

Add the equations (2) and (4) to eliminate the variable y. 

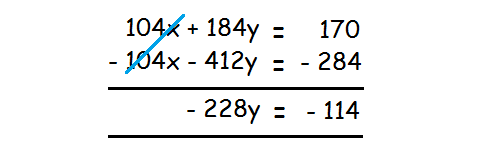
Divide both sides by -228.

-228y / (-228)  =  - 114 / (-228)

y  =  0.5

Step 5 : 

Plug y  =  0.5 in (1) to get the value of x. 

             (1) --------> 52x + 206(0.5)  =  142

52x + 103  =  142

Subtract 103 from both sides. 

52x  =  39

Divide both sides by 52.

52x / 52  =  39 / 52

x  =  0.75

So, the contestants run 0.75 hour and bike 0.5 hour.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.