SOLVING WORD PROBLEMS TRIGONOMETRY

Problem 1 :

A bird is sitting on the top of a 80 m high tree. From a point on the ground, the angle of elevation of the bird is 45° . The bird flies away horizontally in such away that it remained at a constant height from the ground. After 2 seconds, the angle of elevation of the bird from the same point is 30° . Determine the speed at which the bird flies.(√3 = 1.732)

Solution :

Let "x" be the speed at which the bird flies.

Time = distance / speed

2  = distance / x

Distance covered  =  2x

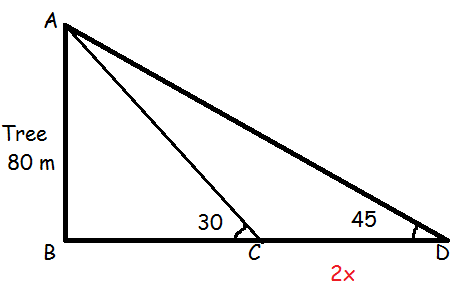
In triangle ABC,

tan θ  =  Opposite side / Adjacent side

tan 30  =  AB / BC

1/√3   =  80/ BC

BC  =  80√3 ----(1)

tan 45  =  AB / CD

1  =  80/(BC + CD)

1  =  80/(BC + 2x)

BC + 2x  =  80

BC  =  80 - 2x   ------(2)

(1)  =  (2)

80√3  =  80 - 2x

By dividing the entire equation by 2, we get

40√3  =  40 - x

x  =  40 - 40√3

x  =  40(1 - 1.732)

x  =  40 (-0.732)

 x = -29.28 

Because, the speed can not be negative, speed of the bird is 29.28 m/s

Problem 2 :

An aeroplane is flying parallel to the Earth’s surface at a speed of 175 m/sec and at a height of 600 m. The angle of elevation of the aeroplane from a point on the Earth’s surface is 37° at a given point. After what period of time does the angle of elevation increase to 53° ? (tan 53° = 1.3270, tan 37° = 0.7536)

Solution :

Let "x" be the required time.

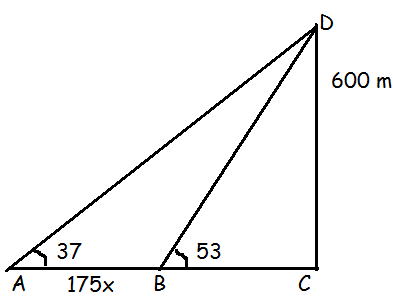
In triangle DBC,

tan 53  =  DC/BC

1.3270  =  600/BC

BC  =  600/1.320 ----(1)

In triangle ADC,

 tan 37  =  DC/AC

 0.7536  =  600/(175x + BC)

175x + BC  =  600/0.7536

BC  =  (600/0.7536) - 175x----(2)

(1)  =  (2)

600/1.3270  =  (600/0.7536) - 175x

175x  =  (600/0.7536) - (600/1.3270)

  175x  =  600(1/0.7536 - 1/1.3270)

  175x  =  600(1.32 - 0.75)

  175x  =  600(0.57)

175x  =  342

x  =  342/175

x  ≈  1.95 seconds

Problem 3 :

A bird is flying from A towards B at an angle of 35° , a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away.

(i) How far is B to the North of A?

(ii) How far is B to the West of A?

(iii) How far is C to the North of B?

(iv) How far is C to the East of B?

(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)

Solution :

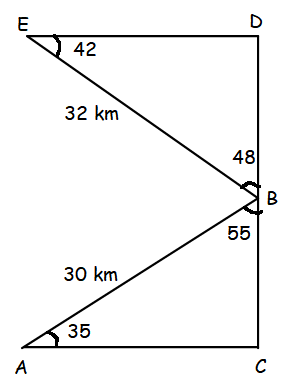
(i)  To find how far is B to the North of A, we should find the length of AC.

sin θ  =  Opposite side/hypotenuse 

cos θ  =  Adjacent side/hypotenuse 

sin 55  =  AC/30

0.8192  =  AC/30

AC  =  0.8192(30)

AC  =  24.58 km

(ii) To find how far is B to the west of A, we should find the length of BC.

cos 55  =  BC/30

0.5736  =  BC/30

BC  =  0.5736(30)

BC  =  17.21 km

(iii) To find how far is C to the north of B, we should find the value of BD.

sin 42  =  BD/32

0.6691  =  BD/32

BD  =  0.6691(32)

BD  =  21.41

(iv) To find how far is C to the east of B, we should find the length of DE. 

cos 42  =  DE/32

0.7341  =  DE/32

DE  =  0.7341(32)

DE  =  23.49 km

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.