SOLVING WORD PROBLEMS USING EQUATIONS

Plan for Solving a Word Problem :

(i)  Find out what numbers are asked for from the given information.

(ii) Choose a variable to represent the number(s) described in the problem. Sketch or a chart may be helpful.

(iii) Write an equation that represents relationships among the numbers in the problem.

(iv)  Solve the equation and find the required numbers.

(v)  Answer the original question. Check that your answer is reasonable.

Cost, Profit and Value Problems

Total Value  =  Number of Items ⋅ Value per Item

Profit  =  Selling Cost - Buying Cost

Example 1 :

A music store owner purchased x compact discs for $6.50 each. He sold all but 19 of them for $12.00 each. If he made a profit of $564.00 from the compact discs, what is the value of x ?

Solution :

The problem asks for the value of x.

x is given as the number of compact discs purchased.

564 = 12x - 228 - 6.5x

Simplify. 

564 = 5.5x - 228

Add 228 to each side. 

792 = 5.5x

Divide each side by 5.5.

144 = x

The number of compact discs purchased is 144.

Distance, Rate and Time Problems

Distance = Rate ⋅ Time

Example 2 :

David drove from his home to the beach at a speed of 50 mph and returned home along the same route at a speed of 30mph. If his total driving time for the trip was two hours, how many minutes did it take him to drive from his home to the beach ?

Solution :

The problem asks for the time it took for David to drive to the beach.

x is given as the number of compact discs purchased.

Let t = the time in hours it took for David to drive to the beach. Then 2 - t = the time spent for the return trip. Make a chart and a sketch showing the given facts.

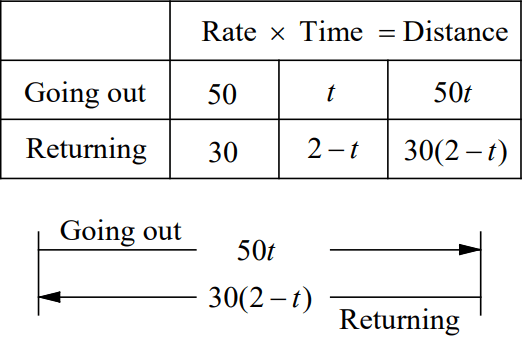
The distance going out = the distance returning.

50t = 30(2 - t)

Distributive property.

50t = 60 - 30t

Add 30t to each side. 

80t = 60

Divide each side by 80.

t = ⁶⁰⁄₈₀

t = ¾ hours

t = ¾ ⋅ 60 minutes

t = 45 minutes

It took David ¾ hours or 45 minutes, to drive from his home to the beach.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.