SOLVING WORD PROBLEMS USING INVERSE MATRIX
Problem 1 :
If
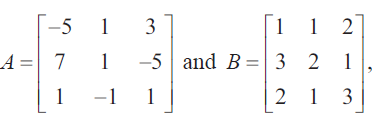
find the products AB and BA and hence solve the system of equations x + y + 2z =1,3x + 2y + z = 7,2x + y + 3z = 2.
Solution :

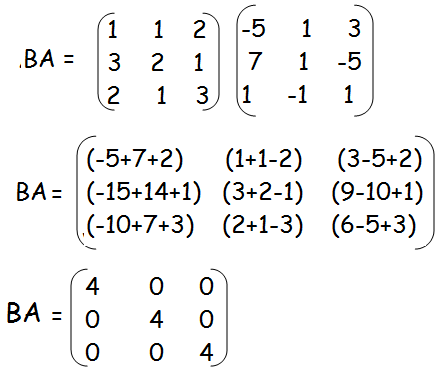
AB = BA
x + y + 2z = 1, 3x + 2y + z = 7, 2x + y + 3z = 2
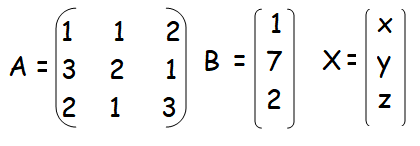
|A| = 1(6 - 1) - 1(9 - 2) + 2(3 - 4)
= 1(5) - 1(7) + 2(-1)
= 5 - 7 - 2
= 5 - 9
= -4
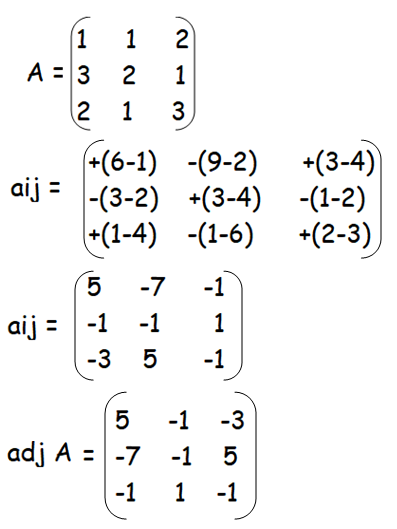
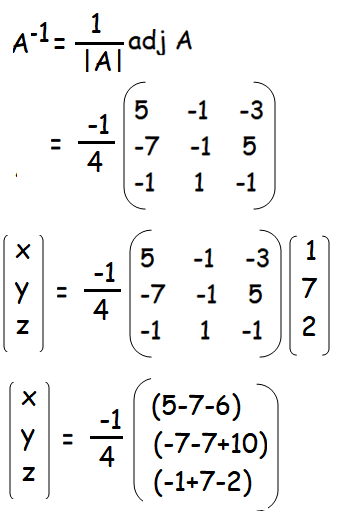
x = (-1/4)(-8) = 2
y = (-1/4)(-4) = 1
y = (-1/4)(4) = -1
So, the values of x, y and z area 2, 1 and -1 respectively.
Problem 2 :
A man is appointed in a job with a monthly salary of certain amount and a fixed amount of annual increment. If his salary was ₹19,800 per month at the end of the first month after 3 years of service and ₹23,400 per month at the end of the first month after 9 years of service, find his starting salary and his annual increment. (Use matrix inversion method to solve the problem.)
Solution :
Let "x" and "y" be the monthly salary and a fixed amount of annual increment respectively.
x + 3y = 19800 ---------(1)
x + 9y = 23400 ---------(2)
X = (1/|A|) adj A
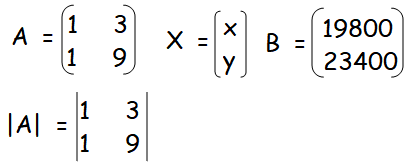
|A| = 9 - 3 = 6
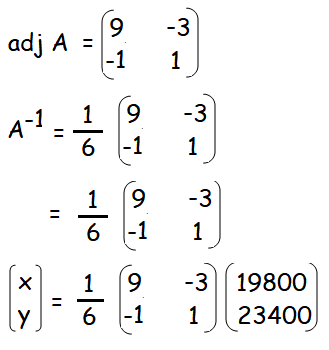
x = (178200 - 70200)/6 = 18000
y = (-19800 + 23400)/6 = 600
So, the monthly salary is 18000 and annual increment is 600.
Problem 3 :
Four men and 4 women can finish a piece of work jointly in 3 days while 2 men and 5 women can finish the same work jointly in 4 days. Find the time taken by one man alone and that of one woman alone to finish the same work by using matrix inversion method.
Solution :
Let "x" be the number of days taken by men and "y" be the number of days taken by women.
One day work done by 1 men = 1/x
One day work done by 1 women = 1/y
(4/x) + (4/y) = (1/3)
(2/x) + (5/y) = (1/4)
1/x = a, 1/y = b
4a + 4b = 1/3 ---(1)
2a + 5b = 1/4 ---(2)
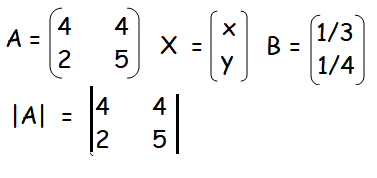
|A| = 20 - 8 = 12
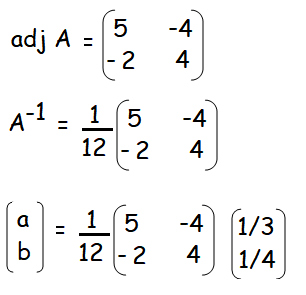
|
a = (1/12) [5/3 - 1] = (1/12) (2/3) a = 1/18 |
b = (1/12) [-2/3 + 1] = (1/12) (1/3) b = 1/36 |
x = 18 and y = 36
So, men can take 18 days to finish the work and women can take 36 days to finish the work.
Problem 4 :
The prices of three commodities A,B and C are ₹ x, y and z per units respectively. A person P purchases 4 units of B and sells two units of A and 5 units of C . Person Q purchases 2 units of C and sells 3 units of A and one unit of B . Person R purchases one unit of A and sells 3 unit of B and one unit of C . In the process, P,Q and R earn ₹ 15,000, ₹ 1,000 and ₹4,000 respectively. Find the prices per unit of A,B and C . (Use matrix inversion method to solve the problem.)
Solution :
2x + 5z - 4y = 15000
3x + y - 2z = 1000
3y + z - x = 4000
2x - 4y + 5z = 15000 --------(1)
3x + y - 2z = 1000 --------(2)
-x + 3y + z = 4000 --------(3)
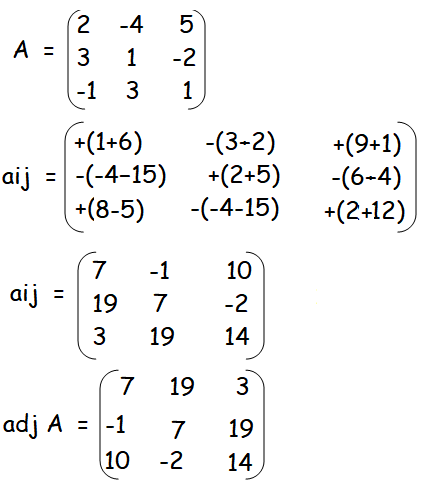
|A| = 2(1 + 6) + 4(3.- 2) + 5(9 + 1)
= 2(7) + 4(1) + 5(10)
= 14 + 4 + 50
|A| = 68
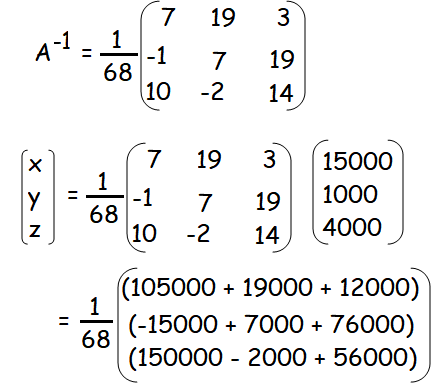
x = (1/68) (136000) = 2000
y = (1/68) (68000) = 1000
z = (1/68) (204000) = 3000
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Eliminating the Parameter in Parametric Equations
Apr 21, 25 10:37 PM
Eliminating the Parameter in Parametric Equations -
Quadratic Equation Problems with Solutions (Part - 3)
Apr 21, 25 02:37 AM
Quadratic Equation Problems with Solutions (Part - 3) -
Digital SAT Math Problems and Solutions (Part - 147)
Apr 20, 25 08:38 AM
Digital SAT Math Problems and Solutions (Part - 147)