SOLVING WORD PROBLEMS WITH CROSS MULTIPLICATION METHOD

Problem 1 :

Places A and B are 100 km apart on a highway. One car starts from A and another from B at the same time. If the car travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of the two cars?

Solution :

Let “x km/hr” be the speed of 1st car

Let “y km/hr” be the speed of the 2nd car

Time  =  Distance/Speed

Speed of both cars while they are traveling in the same direction  =  (x – y)

Speed of both cars while they are traveling in the opposite direction  =  (x + y)

5  =  100/(x -y)

  x – y  =  100/5

x -  y  =  20 

x - y - 20  =  0 ---(1)

1  =  100/(x + y)

x + y  =  100

x +  y - 100  =  0------(2)

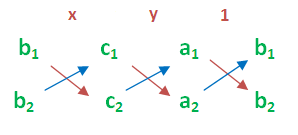
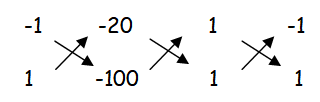
x/(100 + 20)  =  y/(-20 + 100)  =  1/(1 + 1)

x/120  =  y/80  =  1/2

     x/120  = 1/2             y/80  =  1/2

           x = 120/2              y  =  80/2

             x  =  60                 y  =  40

So, the speed of first car  =  60 km/hr

Speed of second car  =  40 km/hr

Problem 2 :

The area of a rectangle gets reduced by 9 square units, if its length is reduced by 5 units and breadth increased by 3 units. If we increase the length by 3 units and the breadth by 2 units, the area increases by 67 square units. Find the dimensions of the rectangle.

Solution :

Area of any rectangle = Length x breadth

Let “x” be the length of rectangle

Let “y” be the breadth of rectangle

(x – 5) (y + 3)  =  xy – 9

x y + 3x -  5y – 15  =  xy – 9

xy – xy  + 3x – 5y – 15 + 9  =  0

3 x – 5 y – 6 = 0 -------(1)

(x + 3) (y + 2) = xy  + 67

xy  + 2x + 3y + 6 – xy – 67 = 0

2x + 3 y – 61 = 0 -------(2)

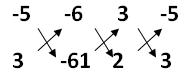
x/(305+18)  =  y/(-12 + 183)  =  1/(9 + 10)

x/323  =  y/171  =  1/19

x/323  =  1/19                y/171  =  1/19

 x  =  323/19                     y  =  171/19

 x  =  17                             y = 9

So, the length of rectangle  =  17 units

Breadth of rectangle   =  9 units

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.