SOLVING WORD PROBLEMS WITH CUBOID

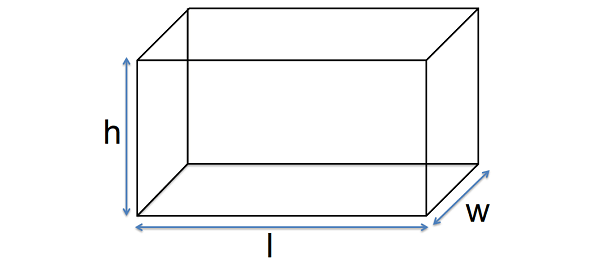
Formulas given below can be used to find volume, lateral surface area and total surface of a cuboid.   

Volume = l x w x h cubic units

Lateral surface area = 2h(l + w) square units

Total surface area = 2(lw + wh + hl) squareunits

Problem 1 :

Find the total surface area and lateral surface area of a cuboid whose length is 20 cm, width is 15 cm and height is 8 cm.

Solution :

Total surface area :

= 2(lw + wh + hl)

Substitute.

= 2[20(15) + 15(8) + 8(20)]

= 2 [300 + 120 + 160]

= 2(580)

= 1160 cm²

Lateral surface area :

= 2h(l + w)

Substitute.

= 2(8)(20 + 15)

= 16(35)

= 560 cm²

Problem 2 :

The dimensions of a cuboidal box are 6 m x 400 cm x 1.5 m. Find the cost of painting its entire outer surface at the rate of $22 per square meter.

Solution :

From the given information,

length (l) = 6 m

width (w) = 400 cm = 400/100 m = 4 m

height = 1.5 m

Outer surface area has six sides.

Then, the required area is

= 2(lw + wh + hl)

Substitute.

= 2[6(4) + 4(1.5) + 1.5(6)]

= 2[24 + 6 + 9]

= 2[39]

= 78 m²

Cost of painting the surface is $22 per m².

So, the required cost is

= 78(22)

 = $1716

Problem 3 :

The dimensions of a hall is 10 m x 9 m x 8 m. Find the cost of white washing the walls and ceiling at the rate of $8.50 per square meter. 

Solution :

From the given information,

length (l) = 10 m

width (w) = 9 m

height = 8 m

Area of white washing is

= 2h(l + w) + lw

Substitute. 

= 2(8)(10 + 9) + 10(9)

= 16(19) + 90

 = 304 + 90

  = 394 m²

Cost of white washing is $8.50 per m².

So, the required cost is

= 394(8.50)

= $3349

Problem 3 :

The dimensions of a hall is 10 m x 9 m x 8 m. Find the cost of white washing the walls and ceiling at the rate of $8.50 per square meter. 

Solution :

From the given information,

length (l) = 10 m

width (w) = 9 m

height = 8 m

Area of white washing is

= 2h(l + w) + lw

Substitute. 

= 2(8)(10 + 9) + 10(9)

= 16(19) + 90

 = 304 + 90

  = 394 m²

Cost of white washing is $8.50 per m².

So, the required cost is

= 394(8.50)

= $3349

Problem 4 :

The length, width and depth of a pond are 20.5 m, 16 m and 8 m respectively. Find the capacity of the pond in liters.

Solution :

l = 20.5 m, w = 16 m, h = 8 m

Capacity of pond : 

= lx w x h

= 20.5(16)(8)

= 2624 m³

1 m³ = 1000 liters, 

= 2624(1000) liters

= 2624000 liters

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.