HOW TO SOLVE POLYNOMIAL EQUATION OF DEGREE 5
To solve a polynomial equation of degree 5, we have to factor the given polynomial as much as possible. After having factored, we can equate factors to zero and solve for the variable.
Example 1 :
Solve :
6x5 - x4 - 43x3 + 43x2 + x - 6 = 0
Solution :
By trial and error, we can check the values 1 or -1 or 2 or -2...... as a zero for the above equation using synthetic division.
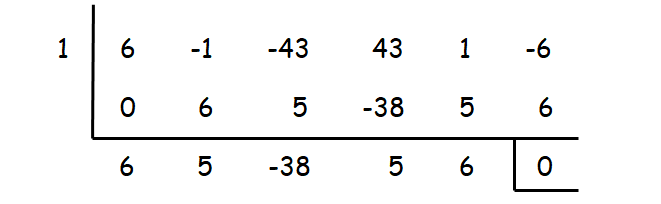
When we check with the value 1, we get remainder zero. So, x = 1 is one of the zeros.
Resulting equation :
6x4 + 5x3 - 38x2 + 5x + 6 = 0
Dividing both sides by x2.
6x4/x2 + 5x3/x2 - 38x2/x2 + 5x/x2 + 6/x2 = 0
6x2 + 5x - 38 + 5/x + 6/x2 = 0
6(x2 + 1/x2) + 5 (x + 1/x) - 38 = 0 ----(1)
Let y = x + 1/x.
y2 = (x + 1/x)2
y2 = x2 + 2(x)(1/x) + (1/x)2
y2 = x2 + 2 + 1/x2
y2 - 2 = x2 + 1/x2
(1)----> 6(y2 - 2) + 5y - 38 = 0
6y2 - 12 + 5y - 38 = 0
6y2 + 5y - 50 = 0
6y2 - 15y + 20 y - 50 = 0
3y(2y - 5) + 10(2y - 5) = 0
(3y + 10)(2y - 5) = 0
|
3y + 10 = 0 y = -10/3 |
2y - 5 = 0 y = 5/2 |
When y = -10/3,
(x2 + 1)/x = -10/3
3(x2 + 1) = -10x
3x2 + 3 = -10x
3x2 + 10x + 3 = 0
(3x + 1)(x + 3) = 0
x = -1/3 and 3
When y = 5/2,
x + 1/x = y
(x2 + 1)/x = 5/2
2(x2 + 1) = 5 x
2x2 + 2 - 5x = 0
2x2 - 5x + 2 = 0
(2x - 1)(x - 2) = 0
x = 1/2 and 2
Therefore the five zeros are 1, -1/3, 3, 1/2 and 2.
Example 2 :
Solve :
8x5 - 22x4 - 55x3 + 55x2 + 22x - 8 = 0
Solution :
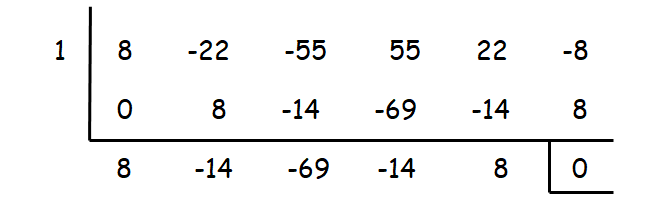
When we check with the value 1, we get remainder zero. So, x = 1 is one of the zeros.
Resulting equation :
8x4 - 14x3 - 69x2 - 14x + 8 = 0
Dividing both sides by x2.
8x4/x2 - 14x3/x2 - 69x2/x2 - 14x/x2 + 8/x2 = 0
8x2 - 14x - 69 - 14/x + 8/x2 = 0
8(x2 + 1/x2) - 14(x + 1/x) - 69 = 0 ----(1)
Let y = x + 1/x.
y2 = (x + 1/x)2
y2 = x2 + 2(x)(1/x) + (1/x)2
y2 = x2 + 2 + 1/x2
y2 - 2 = x2 + 1/x2
(1)----> 8(y2 - 2) - 14y - 69 = 0
8y2 - 16 - 14y - 69 = 0
8y2 - 14y - 85 = 0
(2y + 5)(4y - 17) = 0
|
2y + 5 = 0 y = -5/2 |
4y - 17 = 0 y = 17/4 |
When y = -5/2,
x + 1/x = y
(x2 + 1)/x = -5/2
2(x2 + 1) = -5x
2x2 + 2 + 5x = 0
2x2 + 5x + 2 = 0
2x2 + 4x + 1x + 2 = 0
2x(x + 2) + 1(x + 2) = 0
(2x + 1)(x + 2) = 0
x = -1/2 and -2
When y = 17/4,
x + 1/x = y
(x2 + 1)/x = 17/4
4(x2 + 1) = 17x
4x2 + 4 = 17x
4x2 - 17x + 4 = 0
(4x - 1)(x - 4) = 0
x = 1/4 and 4
Therefore the five zeros are 1, -1/2, -2, 1/4 and 4.
Example 3 :
Solve :
6x5 + 11x4 - 33x3 - 33x2 + 11x + 6 = 0
Solution :
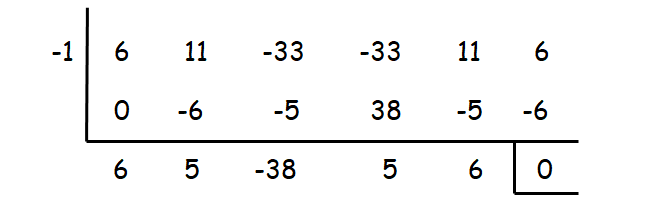
When we check with the value -1, we get remainder zero. So, x = -1 is one of the zeros.
Resulting equation :
6x4 + 5x3 - 38x2 + 5x + 6 = 0
Dividing both sides by x2.
6x4/x2 + 5x3/x2 - 38x2/x2 + 5x/x2 + 6/x2 = 0
6x2 + 5x - 38 + 5/x + 6/x2 = 0
6(x2 + 1/x2) + 5(x + 1/x) - 38 = 0 ----(1)
Let y = x + 1/x.
y2 = (x + 1/x)2
y2 = x2 + 2(x)(1/x) + (1/x)2
y2 = x2 + 2 + 1/x2
y2 - 2 = x2 + 1/x2
(1)----> 6(y2 - 2) + 5y - 38 = 0
6y2 - 12 + 5y - 38 = 0
6y2 + 5y - 50 = 0
6y2 - 15y + 20y - 50 = 0
3y(2y - 5) + 10(2y - 5) = 0
(3y + 10)(2y - 5) = 0
|
3y + 10 = 0 y = -10/3 |
2y - 5 = 0 y = 5/2 |
When y = -10/3,
x + 1/x = y
(x2 + 1)/x = -10/3
3(x2 + 1) = -10x
3x2 + 3 = -10x
3x2 + 10x + 3 = 0
3x2 + 9x + x + 3 = 0
3x(x + 3) + 1(x + 3) = 0
(x + 3)(3x + 1) = 0
x = -3 and -1/3
When y = 5/2,
x + 1/x = y
(x2 + 1)/x = 5/2
2(x2 + 1) = 5x
2x2 + 2 - 5x = 0
2x2 - 5x + 2 = 0
2x2 - 4x - x + 2 = 0
2x(x - 2) - 1(x - 2) = 0
(2x - 1)(x - 2) = 0
x = 1/2 and 2
Therefore the five zeros are -1, -3, -1/3, 1/2 and 2.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 150)
Apr 25, 25 11:46 AM
Digital SAT Math Problems and Solutions (Part - 150) -
AP Calculus AB Problems with Solutions (Part - 19)
Apr 24, 25 11:10 PM
AP Calculus AB Problems with Solutions (Part - 19) -
AP Calculus AB Problems with Solutions (Part - 18)
Apr 24, 25 11:06 PM
AP Calculus AB Problems with Solutions (Part - 18)
