SPEARMAN RANK CORRELATION COEFFICIENT

When we need finding correlation between two qualitative characteristics, say, beauty and intelligence, we take recourse to using rank correlation coefficient.

Rank correlation can also be applied to find the level of agreement (or disagreement) between two judges so far as assessing a qualitative characteristic is concerned.

As compared to product moment correlation coefficient, rank correlation coefficient is easier to compute, it can also be advocated to get a first hand impression about the correlation between a pair of variables.

Spearman’s rank correlation coefficient is given by

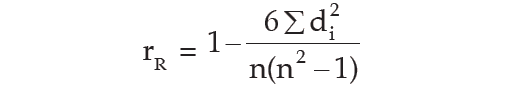
where r_R denotes rank correlation coefficient and it lies between –1 and 1 inclusive of these two values.

d_i = x_i - y_i  represents the difference in ranks for the i^th individual and n denotes the number of individuals.

In case u individuals receive the same rank, we describe it as a tied rank of length u. In case of a tied rank, the above given formula is changed to

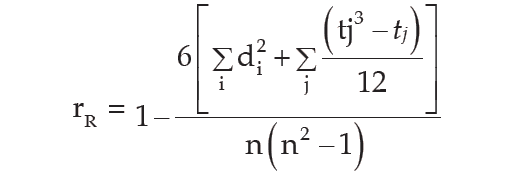
In this formula, t_j represents the j^th tie length and the summation  ∑_i,(t_j³ - t_j) extends over the lengths of all the ties for both the series.

Solved Problems

Problem 1 :

Compute the coefficient of rank correlation between sales and advertisement expressed in thousands of dollars from the following data :

Solution :

Let the rank given to sales be denoted by x and rank of  advertisement be denoted by y.

We note that since the highest sales as given in the data, is 95, it is to be given rank 1, the second highest sales 90 is to be given rank 2 and finally rank 8 goes to the lowest sales, namely 68.

We have given rank to the other variable advertisement in a similar manner. Since there are no ties, we can apply the formula given below.

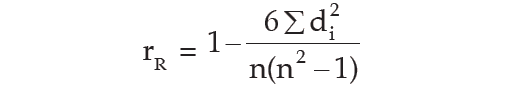
Computation of Rank correlation between Sales and Advertisement.

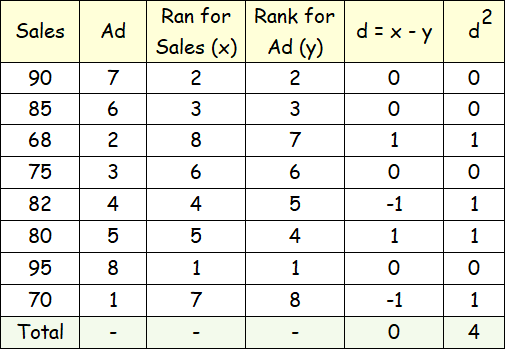
Since n = 8 and ∑d² = 4, apply the above formula, we get 

r = 1 - 6∑d²/n(n² - 1)

= 1 - 6x4/8(8² - 1)

= 1 - 0.0476

= 0.95

The high positive value of the rank correlation coefficient indicates that there is a very good amount of agreement between sales and advertisement.

Problem 2 :

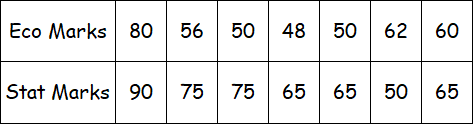
Compute the coefficient of rank correlation between Eco. marks and statistics marks as given below :

Solution :

This is a case of tied ranks as more than one student share the same mark both for Economics and Statistics.

For Eco. the student receiving 80 marks gets rank 1 one getting 62 marks receives rank 2, the student with 60 receives rank 3, student with 56 marks gets rank 4 and since there are two students, each getting 50 marks, each would be receiving a common rank, the average of the next two ranks 5 and 6 i.e. (5 + 6)/2 = 5.50 and lastly the last rank..

7 goes to the student getting the lowest Eco marks.

In a similar manner, we award ranks to the students with stats marks.

Computation of Rank Correlation Between Eco Marks and Stats Marks with Tied Marks

For Economics mark there is one tie of length 2 and for statistics mark, there are two ties of lengths 2 and 3 respectively.

Thus

∑_i,(t_j³ - t_j)/12 = [(2³ - 2) + (2³ - 2) + (3³ - 3)]/12

= [(8 - 2) + (8 - 2) + (27 - 3)]/12

= [6 + 6 + 24]/12

= 36/12

= 3

Spearman’s rank correlation coefficient :

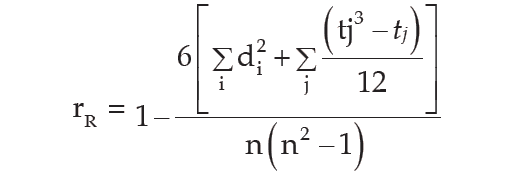
Substitute.

r_R = 1 - [6 x (44.50 + 3)]/[7(7² - 1)]

= 1 - [6 x 47.3)]/[7(49 - 1)]

= 1 - 283.8/336

≈ 0.15

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.