SPECIAL PRODUCTS OF BINOMIALS
Special products are easier ways to find the product of two binominals than multiplying each term in the first binomial with all terms in the second binomial.
Finding the Products in the Form (a + b)²
Imagine a square with sides of length (a + b).
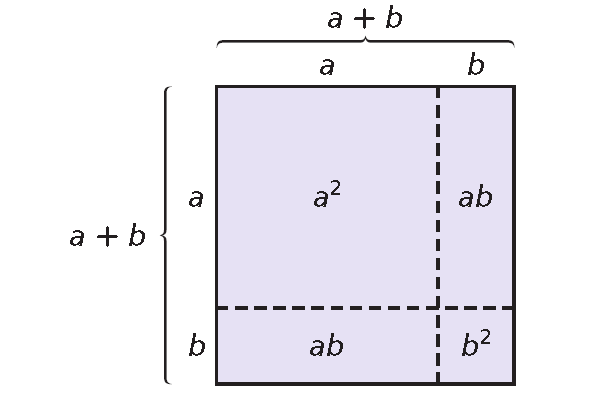
The area of this square is (a + b)(a + b), or (a + b)2. The area of this square can also be found by adding the areas of the smaller squares and rectangles inside.
The sum of the areas inside is
a2 + ab + ab + b2
This means,
(a + b)2 = a2 + 2ab + b2
The FOIL method can be used to verify this.
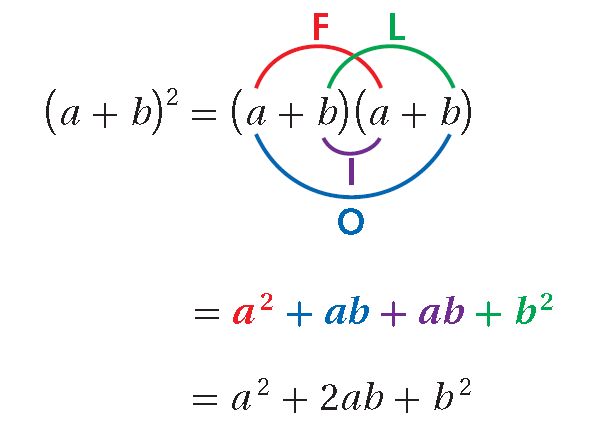
A trinomial of the form a2 + 2ab + b2 is called a perfect-square trinomial. A perfect-square trinomial is a trinomial that is the result of squaring a binomial.
Example 1 :
Expand.
(x + 5)2
Solution :
Use the rule for (a + b)2.
(a + b)2 = a2 + 2ab + b2
Identify a and b : a = x and b = 5.
(x + 5)2 = x2 + 2(x)(5) + 52
= x2 + 10x + 25
Example 2 :
Expand.
(2x + 3y)2
Solution :
Use the rule for (a + b)2.
(a + b)2 = a2 + 2ab + b2
Identify a and b : a = 2x and b = 3y.
(2x + 3y)2 = (2x)2 + 2(2x)(3y) + (3y)2
= 4x2 + 12xy + 9y2
Example 3 :
Expand.
(3 + z2)2
Solution :
Use the rule for (a + b)2.
(a + b)2 = a2 + 2ab + b2
Identify a and b : a = 3 and b = z2.
(3 + z2)2 = (3)2 + 2(3)(z2) + (z2)2
= 9 + 6z2 + z4
Example 4 :
Expand.
(-y + 3)2
Solution :
Use the rule for (a + b)2.
(a + b)2 = a2 + 2ab + b2
Identify a and b : a = -y and b = 3.
(-y + 3)2 = (-y)2 + 2(-y)(3) + (3)2
= y2 - 6y + 9
Finding the Products in the Form (a - b)²
The FOIL method can be used to find products in the form (a - b)2.
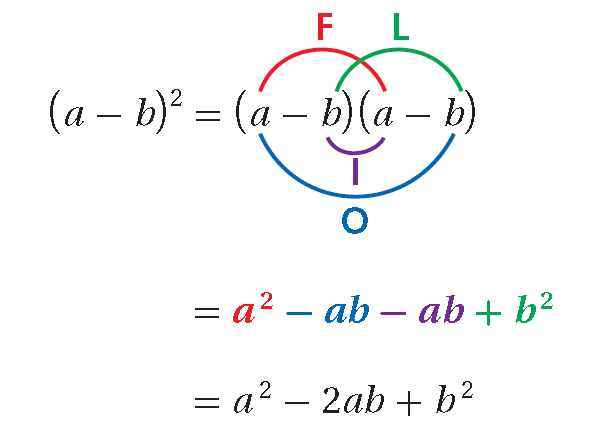
A trinomial of the form a2 - 2ab + b2 is also a perfect-square trinomial, because it is the result of squaring the binomial (a - b)2.
Example 5 :
Expand.
(x - 4)2
Solution :
Use the rule for (a - b)2.
(a - b)2 = a2 - 2ab + b2
Identify a and b : a = x and b = 4.
(x - 4)2 = x2 - 2(x)(4) + 42
= x2 - 8x + 16
Example 6 :
Expand.
(6y - 1)2
Solution :
Use the rule for (a - b)2.
(a - b)2 = a2 - 2ab + b2
Identify a and b : a = 6y and b = 1.
(6y - 1)2 = (6y)2 - 2(6y)(1) + 12
= 36y2 - 12y + 1
Example 7 :
Expand.
(3c - 4d)2
Solution :
Use the rule for (a - b)2.
(a - b)2 = a2 - 2ab + b2
Identify a and b : a = 3c and b = 4d.
(3c - 4d)2 = (3c)2 - 2(3c)(4d) + (4d)2
= 9c2 - 24cd + 16d2
Example 8 :
Expand.
(3 - m2)2
Solution :
Use the rule for (a - b)2.
(a - b)2 = a2 - 2ab + b2
Identify a and b : a = 3 and b = m2.
(3 - m2)2 = (3)2 + 2(3)(m2) + (m2)2
= 9 + 6m2 + m4
Finding the Products in the Form (a + b)(a - b)
An area model can be used to see that
(a + b)(a - b) = a2 - b2
Step 1 :
Begin with a square with area a2. Remove a square with area of b2. The area of the new figure is a2 - b2.
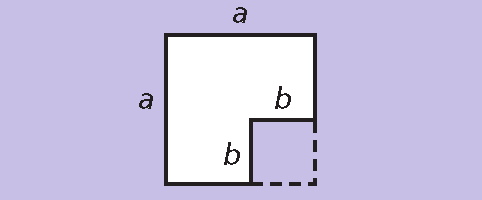
Step 2 :
Then remove the smaller rectangle on the bottom. Turn it side it up next to the top rectangle.
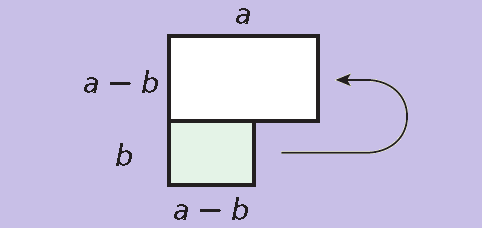
Step 3 :
The new arrangement is a rectangle with length (a + b) and width (a - b). Its area is (a + b)(a - b).
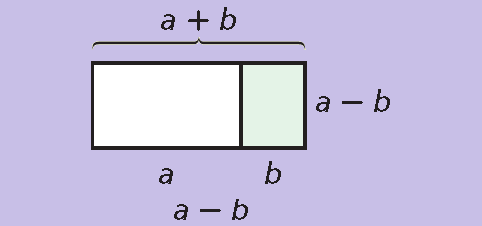
So,
(a + b)(a - b) = a2 - b2
A binomial of the form a2 - b2 is called a difference of two squares.
Example 9 :
Multiply.
(x + y)(x - y)
Solution :
Use the rule for (a + b)(a - b).
(a + b)(a - b) = a2 - b2
Identify a and b : a = x and b = y.
(x + y)(x - y) = x2 - y2
Example 10 :
Multiply.
(y + 5)(y - 5)
Solution :
Use the rule for (a + b)(a - b).
(a + b)(a - b) = a2 - b2
Identify a and b : a = y and b = 5.
(y + 5)(y - 5) = y2 - 52
= y2 - 25
Example 11 :
Multiply.
(p2 + 2q)(p2 - 2q)
Solution :
Use the rule for (a + b)(a - b).
(a + b)(a - b) = a2 - b2
Identify a and b : a = p2 and b = 2q.
(p2 + 2q)(p2 - 2q) = (p2)2 - (2q)2
= p4 - 4q2
Example 12 :
Multiply.
(8 + m)(8 - m)
Solution :
Use the rule for (a + b)(a - b).
(a + b)(a - b) = a2 - b2
Identify a and b : a = 8 and b = m.
(8 + m)(8 - m) = (8)2 - (m)2
= 64 - m2
Problem-Solving Application
Example 13 :
A square koi pond is surrounded by a gravel path. Write an expression that represents the area of the path.
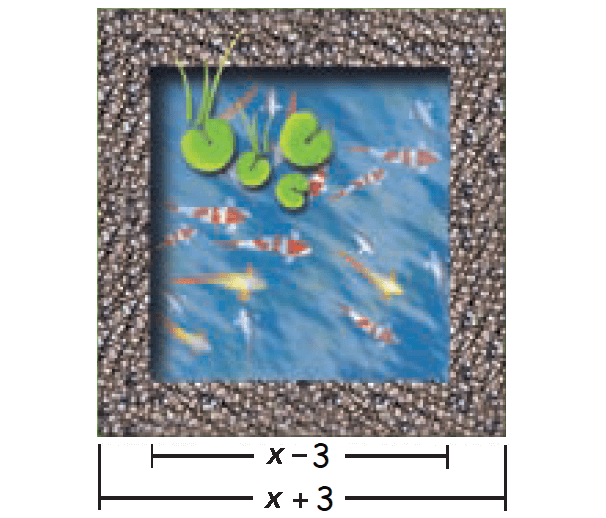
Solution :
Understand the Problem
The answer will be an expression that represents the area of the path.
List the important information :
(i) The pond is a square with a side length of (x - 3).
(ii) The path has a side length of (x + 3).
Make a Plan
The area of the pond is (x - 3)2. The total area of the path plus the pond is (x + 3)2. You can subtract the area of the pond from the total area to find the area of the path.
Solve
Step 1 :
Find the total area.
Use the rule for (a + b)2.
(a + b)2 = a2 + 2ab + b2
Identify a and b : a = x and b = 3.
(x + 3)2 = (x)2 + 2(x)(3) + (3)2
= x2 + 6x + 9
Step 2 :
Find the area of the pond.
Use the rule for (a - b)2.
(a - b)2 = a2 - 2ab + b2
Identify a and b : a = x and b = 3.
(x - 3)2 = (x)2 - 2(x)(3) + (3)2
= x2 - 6x + 9
Step 3 :
Find the area of the path.
Area of Path = Total Area - Area of Pond
= (x2 + 6x + 9) - (x2 - 6x + 9)
Use the Distributive Property.
= x2 + 6x + 9 - x2 + 6x - 9
Group like terms together.
= (x2 - x2) + (6x + 6x) + (9 - 9)
Combine like terms.
= 12x
The area of the path is 12x.
Special Products of Binomials
Perfect-Square Trinomials :
(a + b)2 = (a + b)(a + b) = a2 + 2ab + b2
(a - b)2 = (a - b)(a - b) = a2 - 2ab + b2
Difference of Two Squares :
(a + b)(a - b) = a2 - b2
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 103)
Jan 25, 25 01:00 AM
Digital SAT Math Problems and Solutions (Part - 103) -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Jan 25, 25 12:52 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 102)
Jan 24, 25 12:30 PM
Digital SAT Math Problems and Solutions (Part - 102)