SIMPLIFYING SQUARE ROOTS
The following steps will be useful to simplify any square root.
(i) Decompose the number inside the square root into prime factors.
(ii) Inside the square root, if the same number is repeated twice with multiplication, it can be taken out of the square root.
(iii) Combine the like square root terms using mathematical operations.
Example :
√27 + √3 - √12 = √(3 ⋅ 3 ⋅ 3) + √3 - √(2 ⋅ 2 ⋅ 3)
= 3√3 + √3 - 2√3
= 2√3
Solved Questions
Simplify each the following square root expressions :
Question 1 :
√64 + √196
Answer :
Because 64 and 196 are perfect squares, we can find the square root of 64 and 194 as shown below.
|
√64 = √(8 ⋅ 8) √64 = 8 |
√196 = √(14 ⋅ 14) √196 = 14 |
√64 + √196 = 8 + 14
= 22
Question 2 :
√40 + √160
Answer :
Decompose 40 and 160 into prime factors using synthetic division.
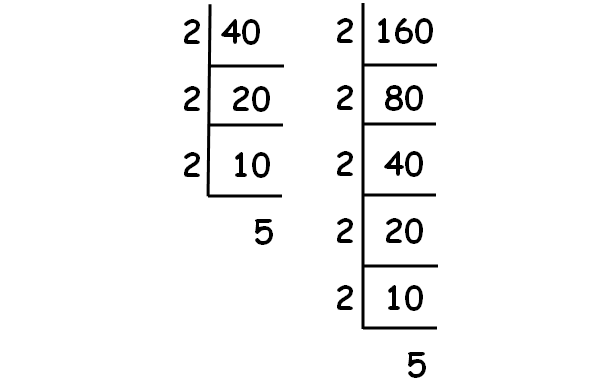
√40 = √(2 ⋅ 2 ⋅ 2 ⋅ 5) = 2√10
√160 = √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 5) = 4√10
√40 + √160 :
= 2√10 + 4√10
= 6√10
Question 3 :
2√425 - 3√68
Answer :
Decompose 425 and 68 into prime factors using synthetic division.
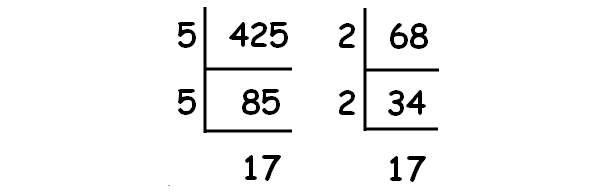
|
√425 = √(5 ⋅ 5 ⋅ 17) √425 = 5√17 |
√68 = √(2 ⋅ 2 ⋅ 17) √68 = 2√17 |
2√425 - 3√68 :
= 2(5√17) - 3(2√17)
= 10√17 - 6√17
= 4√17
Question 4 :
√243 - 5√12 + √27
Answer :
Decompose 243, 12 and 27 into prime factors using synthetic division.
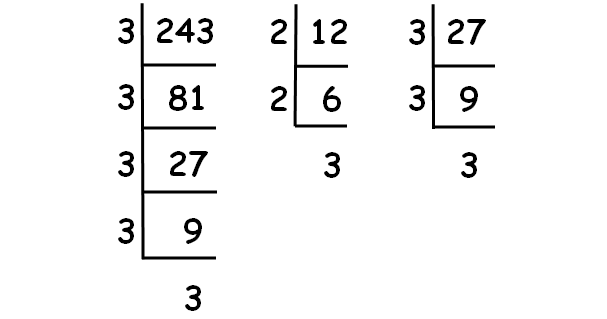
√243 = √(3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3) = 9√3
√12 = √(2 ⋅ 2 ⋅ 3) = 2√3
√27 = √(3 ⋅ 3 ⋅ 3) = 3√3
√243 - 5√12 + √27 :
= 9√3 - 5(2√3) + 3√3
= 9√3 - 10√3 + 3√3
= 2√3
Question 5 :
-√117 - √52
Answer :
Decompose 117 and 52 into prime factors using synthetic division.
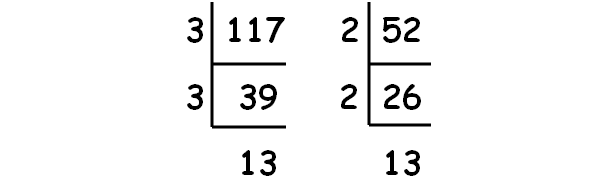
√117 = √(3 ⋅ 3 ⋅ 13) = 3√13
√52 = √(2 ⋅ 2 ⋅ 13) = 2√13
-√117 - √52 :
= -3√13 - 2√13
= -5√13
Question 6 :
(√17)(√51)
Answer :
Decompose 17 and 51 into prime factors.
Because 17 is a prime number, it can't be decomposed anymore. So, √17 has to be kept as it is.
√51 = √(3 ⋅ 17) = √3 ⋅ √17
(√17)(√51) :
= (√17)(√3 ⋅ √17)
= (√17 ⋅ √17)√3
= 17√3
Question 7 :
(√35)(2√15)
Answer :
(√35)(2√15)
Decompose 35 and 15 into prime factors.
√35 = √(5 ⋅ 7) = √5 ⋅ √7
√15 = √(5 ⋅ 3) = √5 ⋅ √3
(√35)(2√15) :
= (√5 ⋅ √7) ⋅ 2(√5 ⋅ √3)
= 2(√5 ⋅ √5)(√7 ⋅ √3)
= 2(5)(√(7 ⋅ 3)
= 10√21
Question 8 :
(14√117) ÷ (7√52)
Answer :
Decompose 117 and 52 into prime factors using synthetic division.
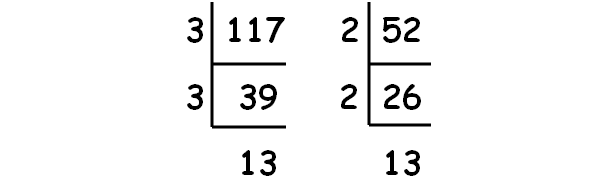
|
√117 = √(3 ⋅ 3 ⋅ 13) √117 = 3√13 |
√52 = √(2 ⋅ 2 ⋅ 13) √52 = 2√13 |
(14√117) ÷ (7√52) :
= 14(3√13) ÷ 7(2√13)
= 42√13 ÷ 14√13
= 42√13/14√13
= 3
Question 9 :
(7√5)2
Answer :
(7√5)2 = 7√5 ⋅ 7√5
= (7 ⋅ 7)(√5 ⋅ √5)
= (49)(5)
= 245
Question 10 :
(√3)3 + √27
Answer :
(√3)3 + √27 = (√3 ⋅ √3 ⋅ √3) + √(3 ⋅ 3 ⋅ 3)
= (3 ⋅ √3) + 3√3
= 3√3 + 3√3
= 6√3
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
AP Calculus AB Problems with Solutions (Part - 8)
Jan 30, 25 09:48 AM
AP Calculus AB Problems with Solutions (Part - 8) -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Jan 29, 25 06:00 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 105)
Jan 29, 25 05:52 AM
Digital SAT Math Problems and Solutions (Part - 105)
