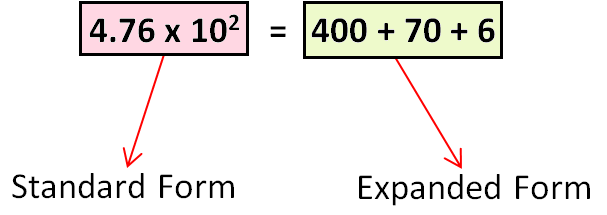
STANDARD AND EXPANDED FORM OF NUMBERS

Standard Form of a Number :

Writing a number in standard form follows certain rules. Any number that is written as a decimal number between 1.0 and 10.0, multiplied by a power of 10, is said to be in standard form.

Examples :

1.23 x 10²

3.5 x 10^-3

2.0 x 10⁵

Expanded Form of a Number :

To write an ordinary number in expanded form, each digit in the ordinary number has to be multiplied by the corresponding place value.

Example :

758 = 7x100 + 5x10 + 8x1

= 700 + 50 + 8

The expanded form of 758 is 700 + 50 + 8.

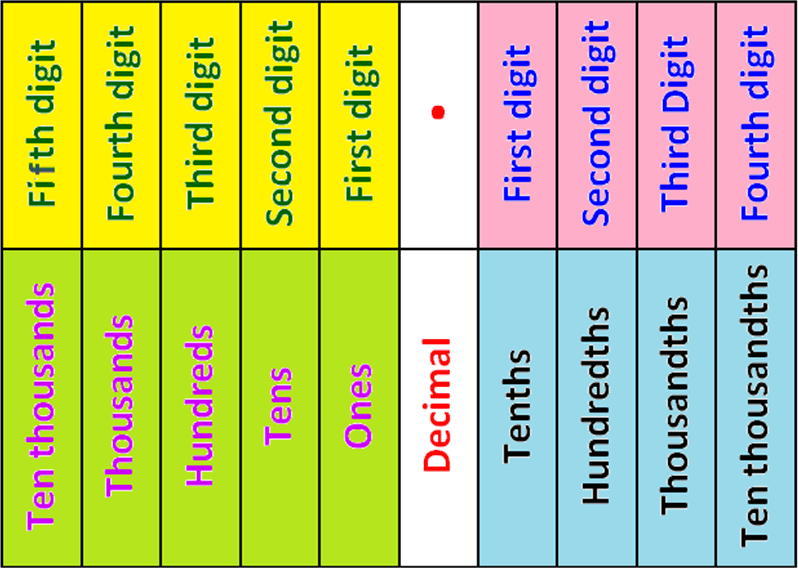
Place Value Chart

Solved Examples

Examples 1-10 : Write the given number in expanded form.

Example 1 :

6523

Solution :

Multiply each digit of 6523 by its corresponding place value.

6523 = 6x1000 + 5x100 + 2x10 + 3x1

= 6000 + 500 + 20 + 3

Example 2 :

758.23

Solution :

Multiply each digit of 758.23 by its corresponding place value.

758.23 :

= 7x100 + 5x10 + 8x1 + 2x¹⁄₁₀ + 3x¹⁄₁₀₀

= 700 + 50 + 8 + ²⁄₁₀ + ³⁄₁₀₀

= 700 + 50 + 8 + 0.2 + 0.03

Example 3 :

652973

Solution :

652973 = 600000 + 50000 + 2000 + 900 + 70 + 3

Example 4 :

0.287

Solution :

0.287 = 0.2 + 0.08 + 0.007

Example 5 :

0.00807

Solution :

0.00807 = 0.008 + 0.00007

Example 6 :

2.53794 x 10⁵

Solution :

2.53794 x 10⁵ = 253794

= 200000 + 50000 + 3000 + 700 + 90 + 4

Example 7 :

3.4567 x 10²

Solution :

3.4567 x 10² = 345.67

= 300 + 40 + 5 + 0.6 + 0.07

Example 8 :

3.8 x 10³

Solution :

3.8 x 10³ = 3800

= 3000 + 800

Example 9 :

7.4 x 10^-5

Solution :

7.4 x 10^-5 = 0.000074

= 0.00007 + 0.000004

Example 10 :

2.5678 x 10^-3

Solution :

2.5678 x 10^-3 = 0.0025678

= 0.002 + 0.0005 + 0.00006 + 0.000007 + 0.0000008

Examples 11-23 : Write the given number in standard form.

Example 11 :

900 + 70 + 2

Solution :

900 + 70 + 2 = 972

In 972, there is no decimal point. So, assume there is decimal point at the end.

= 972. ----(1)

Take decimal point right after the first nonzero digit.

= 9.72 ----(2)

Compare (1) and (2), count the number of digits that the decimal point is shifted. The decimal point is shifted two digits to the left. Take 2 as exponent for 10 and multiply 9.72 by 10² to write the given number in standard form.

900 + 70 + 2 = 9.72 x 10² 

Example 12 :

4000 + 200 + 30 + 5 + 0.9 + 0.01

Solution :

4000 + 200 + 30 + 5 + 0.9 + 0.01 = 4235.91

= 4.23591 x 10³

Example 13 :

0.0003 + 0.00005 + 0.000009

Solution :

0.0003 + 0.00005 + 0.000009 = 0.000359

= 0.000359 ----(1)

Take decimal point right after the first nonzero digit.

= 3.59 ----(2)

Compare (1) and (2), count the number of digits that the decimal point is shifted. The decimal point is shifted four digits to the right. Take -4 as exponent for 10 and multiply 3.592 by 10^-4 to write the given number in standard form.

0.0003 + 0.00005 + 0.000009 = 3.59 x 10^-4

Example 14 :

2 + 0.5

Solution :

2 + 0.5 = 2.5

2 + 0.5 = 2.5 x 10⁰

Example 15 :

30 + 7 + 0.03

Solution :

30 + 7 + 0.03 = 37.03

= 3.703 x 10¹

Example 16 :

50000 + 7000 + 900 + 20 + 3

Solution :

50000 + 7000 + 900 + 20 + 3 = 57923

= 5.7923 x 10⁴

Example 17 :

8000 + 600 + 4

Solution :

8000 + 600 + 4 = 8604

= 8.604 x 10³

Example 18 :

9000 + 1 + 0.003 + 0.00004

Solution :

9000 + 1 + 0.003 + 0.00004 = 9001.00304

= 9.00100304 x 10³

Example 19 :

0.1 + 0.002 + 0.00003

Solution :

0.1 + 0.002 + 0.00003 = 0.10203

= 1.0203 x 10^-1

Example 20 :

0.02 + 0.0005 + 0.000007

Solution :

0.02 + 0.0005 + 0.000007 = 0.020507

= 2.0507 x 10^-2

Example 21 :

7x10000 + 4x1000 + 3x10 + 9x1

Solution :

7x10000 + 4x1000 + 3x10 + 9x1 = 70000 + 4000 + 30 + 9

= 74039

= 7.4039 x 10⁴

Example 22 :

3x10^-1 + 5x10^-2 + 1x10^-3 + 4x10^-4

Solution :

3x10^-1 + 5x10^-2 + 1x10^-3 + 4x10^-4 :

= 3x¹⁄₁₀ + 5x¹⁄₁₀₀ + 1x¹⁄₁₀₀₀ + 4x¹⁄₁₀₀₀₀

= ³⁄₁₀ + ⁵⁄₁₀₀ + ¹⁄₁₀₀₀ + ⁴⁄₁₀₀₀₀

= 0.3 + 0.05 + 0.001 + 0.0004

= 0.3514

= 3.514 x 10^-1

Example 23 :

9x10² + 8x10¹ + 7x10⁰ + 6x10^-1 + 5x10^-2

Solution :

9x10² + 8x10¹ + 7x10⁰ + 6x10^-1 + 5x10^-2 :

= 9x100 + 8x10 + 7x1 + 6x¹⁄₁₀ + 5x¹⁄₁₀₀

= 900 + 80 + 7 + ⁶⁄₁₀ + ⁵⁄₁₀₀

= 900 + 80 + 7 + 0.6 + 0.05

= 987.65

= 9.8765 x 10²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.