STANDARD DEVIATION FOR GROUPED DATA
Standard Deviation for Discrete Frequency Distribution
Mean Method :
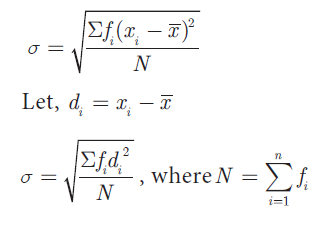
Assumed Mean Method :
Let x1, x2, x3, ...........xn be the observations in the given data with frequencies f1, f2,f3, .......fn respectively. Let x bar be their mean and A be the assumed mean.
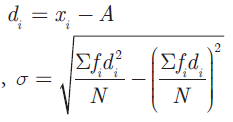
Standard Deviation for Continuous Frequency Distribution
Mean Method :
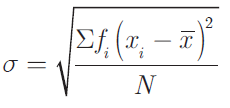
where xi = Middle value of the ith class.
fi = Frequency of the ith class
Step Deviation Method :
To make the calculation simple, we provide the following formula. Let A be the assumed mean, xi be the middle value of the ith class and c is the width of the class interval.
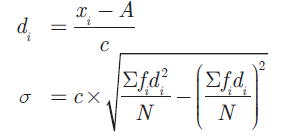
Example 1 :
The rainfall recorded in various places of five districts in a week are given below.
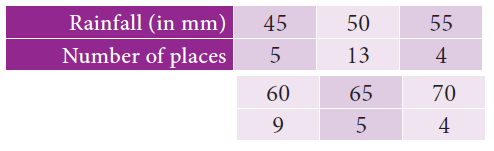
Solution :
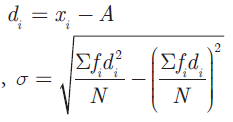
|
x 45 50 55 60 65 70 |
d =x-A d=x-55 -10 -5 0 5 10 15 |
f 5 13 4 9 5 4 |
d2 100 25 0 25 100 225 |
fd2 500 325 0 225 500 900 |
fd -50 -65 0 45 50 60 |
Σf = N = 40
Σfd2 = 2450
(Σfd2/N) = (2450/40)
Σfd = 40
(Σfd/N)2 = (40/40)2 = 1
σ = √(245/4) - 1
σ = √(245-4)/4
σ = √(241/4)
σ = √60.25
σ = 7.76
Example 2 :
In a study about viral fever, the number of people affected in a town were noted as

Find its standard deviation.
Solution :
|
x 5 15 25 35 45 55 65 |
d =x-A d=(x-35)/5 -6 -4 -2 0 2 4 6 |
f 3 5 16 18 12 7 4 |
d2 36 16 4 0 4 16 36 |
fd2 108 80 64 0 48 112 144 |
fd -18 -20 -32 0 24 28 24 |
Σf = N = 65
Σfd2 = 556
(Σfd2/N) = (556/65) = 8.55
Σfd = 6 = Σfd/N = 6/65 = 0.09
σ = √(8.55 - 0.09) ⋅ 5
σ = (√8.46) ⋅ 5
σ = (2.91) ⋅ 5
σ = 14.55
The standard deviation is approximately 14.6.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 150)
Apr 25, 25 11:46 AM
Digital SAT Math Problems and Solutions (Part - 150) -
AP Calculus AB Problems with Solutions (Part - 19)
Apr 24, 25 11:10 PM
AP Calculus AB Problems with Solutions (Part - 19) -
AP Calculus AB Problems with Solutions (Part - 18)
Apr 24, 25 11:06 PM
AP Calculus AB Problems with Solutions (Part - 18)
