STANDARD FORM TO VERTEX FORM OF A QUADRATIC FUNCTION WORKSHEET

Problem 1 :

Write the following quadratic function in vertex form and sketch the parabola.

y  =  x² - 4x + 3

Problem 2 :

Write the following quadratic function in vertex form and sketch the parabola.

y  =  2x² - 8x + 9

Detailed Answer Key

Problem 1 :

Write the following quadratic function in vertex form and sketch the parabola.

y  =  x² - 4x + 3

Solution :

Step 1 :

In the quadratic function given, the coefficient of x² is 1. So, we can skip step 1. 

Step 2 :

In the quadratic function y  =  x² - 4x + 3, write the "x" term as a multiple of 2. 

Then, 

y  =  x² - 2(x)(2) + 3

Step 3 :

Now add and subtract 2² on the right side to complete the square.  

Then, 

y  =  x² - 2(x)(2) + 2² - 2² + 3

y  =  x² - 2(x)(2) + 2² - 4 + 3

y  =  x² - 2(x)(2) + 2² - 1

Step 4 :

In the result of step 3, if we use the algebraic identity

(a - b)²  =  a² - 2ab + b²

on the right side, we get

y  =  (x - 2)² - 1

The quadratic function above is in vertex form. 

Comparing 

y  =  (x - 2)² - 1

and

y  =  a(x - h)² + k,

the vertex is

(h, k)  =  (2, -1)

and

a  =  1

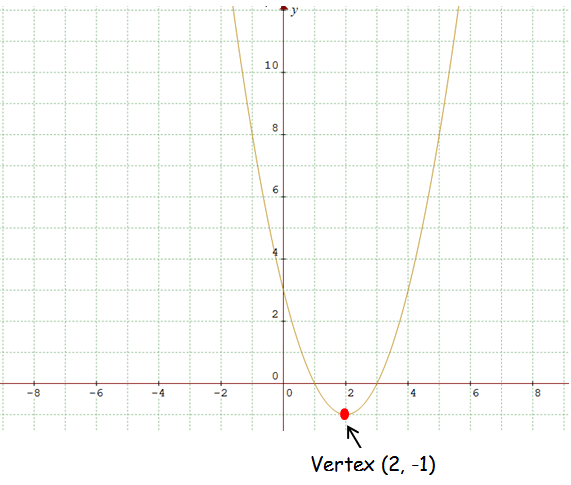
Graph of the Parabola :

The vertex of the parabola is (2, -1). Because the sign of "a" is positive the parabola opens upward.

Problem 2 :

Write the following quadratic function in vertex form and sketch the parabola.

y  =  2x² - 8x + 9

Solution :

Step 1 :

In the quadratic function given, the coefficient of x² is 2. So, factor "2" from the first two terms of the quadratic expression on the right side.

y  =  2(x² - 4x) + 9

Step 2 :

In the quadratic function y  =  2(x² - 4x) + 9, write the "x" term as a multiple of 2. 

Then, 

y  =  2[x² - 2(x)(2)] + 9

Step 3 :

Now add and subtract 2² inside the parentheses to complete the square. 

Then, 

y  =  2[x² - 2(x)(2)+ 2² - 2²] + 9

y  =  2[x² - 2(x)(2)+ 2² - 4] + 9

Step 4 :

In the result of step 3, if we use the algebraic identity

(a - b)²  =  a² - 2ab + b²

inside the parentheses, we get

y  =  2[(x - 2)² - 4] + 9

y  =  2(x - 2)² - 8 + 9

y  =  2(x - 2)² + 1

The quadratic function above is in vertex form. 

Comparing 

y  =  2(x - 2)² + 1

and

y  =  a(x - h)² + k,

the vertex is

(h, k)  =  (2, 1)

and

a  =  2

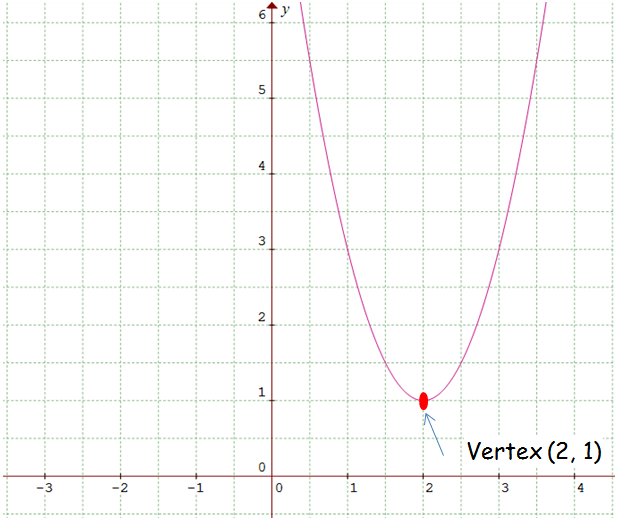
Graph of the Parabola :

The vertex of the parabola is (2, 1). Because the sign of "a" is positive the parabola opens upward.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.