STATISTICAL DEFINITION OF PROBABILITY

Owing to the limitations of the classical definition of probability, there are cases when we consider the statistical definition of probability based on the concept of relative frequency.

This definition of probability was first developed by the British mathematicians in connection with the survival probability of a group of people.

Probability - A Statistical Definition

Let us consider a random experiment repeated a very good number of times, say "n", under an identical set of conditions.

We next assume that an event A occurs "F" times.

Then the limiting value of the ratio of "F" to "n" as "n" tends to infinity is defined as the probability of A.

That is

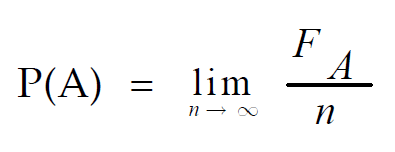
This statistical definition is applicable if the above limit exists and tends to a finite value.

Example :

The following data relate to the distribution of wages of a group of workers :

If a worker is selected at random from the entire group of workers, what is the probability that

(a) his wage would be less than $ 50 ?

(b) his wage would be less than $ 80 ?

(c) his wage would be more than $ 100 ?

(d) his wages would be between $ 70 and $ 100 ?

Solution :

(a) Since there is no worker with wage less than $ 50, the probability that the wage of a randomly selected worker would be less than $ 50 is

P(A)  =  0

(b) Since there are (15+23+36) or 74 worker having wages less than $ 80 out of a group of 150 workers, the probability that the wage of a worker, selected at random from the group, would be less than $ 80 is

P(B)  =  74/150

P(B)  =  37/75

(c) There are (12+5) or 17 workers with wages more than $ 100.

Thus the probability of finding a worker, selected at random, with wage more than $ 100 is

P(C)  =  17/150

(d)  There are (36+42+17) or 95 workers with wages in between $ 70 and $ 100. Thus

P(D)  =  95/150

P(D)  =  19/30

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.